Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-23T05:14:25.266Z Has data issue: false hasContentIssue false
  • English
  • Français

GROWTH ESTIMATES FOR WARPING FUNCTIONS AND THEIR GEOMETRIC APPLICATIONS

Published online by Cambridge University Press:  01 September 2009

BANG-YEN CHEN  and
SHIHSHU WALTER WEI
BANG-YEN CHEN
Affiliation:
Department of Mathematics, Michigan State University, East Lansing, MI 48824-1027, USA e-mail: [email protected]
SHIHSHU WALTER WEI
Affiliation:
Department of Mathematics, University of Oklahoma, Norman, OK 73019-0315, USA e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

By applying Wei, Li and Wu's notion (given in ‘Generalizations of the uniformization theorem and Bochner's method in p-harmonic geometry’, Comm. Math. Anal. Conf., vol. 01, 2008, pp. 46–68) and method (given in ‘Sharp estimates on -harmonic functions with applications in biharmonic maps, preprint) and by modifying the proof of a general inequality given by Chen in ‘On isometric minimal immersion from warped products into space forms’ (Proc. Edinb. Math. Soc., vol. 45, 2002, pp. 579–587), we establish some simple relations between geometric estimates (the mean curvature of an isometric immersion of a warped product and sectional curvatures of an ambient m-manifold 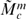bounded from above by a non-positive number c) and analytic estimates (the growth of the warping function). We find a dichotomy between constancy and ‘infinity’ of the warping functions on complete non-compact Riemannian manifolds for an appropriate isometric immersion. Several applications of our growth estimates are also presented. In particular, we prove that if f is an Lq function on a complete non-compact Riemannian manifold N1 for some q > 1, then for any Riemannian manifold N2 the warped product N1 ×fN2 does not admit a minimal immersion into any non-positively curved Riemannian manifold. We also show that both the geometric curvature estimates and the analytic function growth estimates in this paper are sharp.

Keywords

Primary 26D1053C42secondary 31B0553C21
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 51 , Issue 3 , September 2009 , pp. 579 - 592
Copyright
Copyright © Glasgow Mathematical Journal Trust 2009

References

REFERENCES

1.Andreotti, A. and Vesentini, E., Carleman estimates for the Laplace–Beltrami equation on complex manifolds, Inst. Hautes Tudes Sci. Publ. Math. 25 (1965), 81–130.Google Scholar
2.Chen, B. Y., Geometry of submanifolds (M. Dekker, New York, 1973).Google Scholar
3.Chen, B. Y., Some pinching and classification theorems for minimal submanifolds, Arch. Math. 60 (1993), 568–578.CrossRefGoogle Scholar
4.Chen, B.Y., Some new obstructions to minimal and Lagrangian isometric immersions, Jpn J. Math. 26 (2000), 105–127.Google Scholar
5.Chen, B. Y., On isometric minimal immersion from warped products into space forms, Proc. Edinb. Math. Soc. 45 (2002), 579–587.Google Scholar
6.Chen, B. Y., δ-invariants, inequalities of submanifolds and their applications, in Topics in Differential Geometry (Mihai, A, Mihai, I and Miron, R, Editors), (Editura Academiei Române, Bucharest, Romania, 2008), 29–155.Google Scholar
7.Chen, B. Y. and Wei, S. W., Submanifolds of warped product manifolds I ×f S m−1(k) from a p-harmonic viewpoint, Bull. Transilv. Univ. Braşov Ser. III, 1 (50) (2008), 59–78.Google Scholar
8.Karp, L., Subharmonic functions on real and complex manifolds, Math. Z. 179 (1982), 535–554.Google Scholar
9.Wei, S. W., Li, J. and Wu, L., Generalizations of the uniformization theorem and Bochner's method in p-harmonic geometry, Comm. Math. Anal. Conf. 01 (2008), 46–68.Google Scholar
10.Wei, S. W., Li, J. F. and Wu, L., Sharp estimates on -harmonic functions with applications in biharmonic maps, preprint.Google Scholar
11.Wei, S. W., p-harmonic geometry and related topics, Bull. Transilv. Univ. Brasov Ser. III 1 (50) (2008), 415–453.Google Scholar