Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-24T02:17:20.461Z Has data issue: false hasContentIssue false
  • English
  • Français

GROWTH CONDITIONS FOR OPERATORS WITH SMALLEST SPECTRUM

Part of: Entire and meromorphic functions, and related topics General theory of linear operators

Published online by Cambridge University Press:  18 December 2014

H. S. MUSTAFAYEV
H. S. MUSTAFAYEV*
Affiliation:
Department of Mathematics, Faculty of Sciences, Yuzuncu Yil University, Van 65080, Turkey e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let A be an invertible operator on a complex Banach space X. For a given α ≥ 0, we define the class 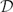$\mathcal{D}$Aα(ℤ) (resp. 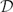$\mathcal{D}$Aα (ℤ+)) of all bounded linear operators T on X for which there exists a constant CT>0, such that

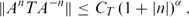$ \begin{equation*} \Vert A^{n}TA^{-n}\Vert \leq C_{T}\left( 1+\left\vert n\right\vert \right) ^{\alpha }, \end{equation*} $
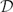for all n ∈ ℤ (resp. n∈ ℤ+). We present a complete description of the class $\mathcal{D}$Aα (ℤ) in the case when the spectrum of A is real or is a singleton. If T ∈ 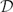$\mathcal{D}$A(ℤ) (=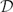$\mathcal{D}$A0(ℤ)), some estimates for the norm of AT-TA are obtained. Some results for the class 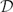$\mathcal{D}$Aα (ℤ+) are also given.

MSC classification

Primary: 47A11: Local spectral properties
Secondary: 30D20: Entire functions, general theory
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 57 , Issue 3 , September 2015 , pp. 665 - 680
Copyright
Copyright © Glasgow Mathematical Journal Trust 2014 

References

REFERENCES

1.Beauzamy, B., Introduction to operator theory and invariant subspaces (North-Holland, Amsterdam, 1988).Google Scholar
2.Benedetto, J., Harmonic analysis on totally disconnected sets, Lecture Notes in Mathematics, vol. 202, (Springer, Berlin-Heidelberg-New York, 1971).CrossRefGoogle Scholar
3.Boas, R. P., Entire functions (Academic Press, New York, 1954).Google Scholar
4.Bonsall, F. F. and Duncan, J., Complete normed algebras, vol. 80, (Springer-Verlag, Berlin, 1973).CrossRefGoogle Scholar
5.Colojoară, I. and Foiaş, C., Theory of generalized spectral operators (Gordon and Breach, New York, 1968).Google Scholar
6.Deddens, J. A., Another description of nest algebras in Hilbert spaces operators Lect. Notes Math. 693 (1978), 77–86.CrossRefGoogle Scholar
7.Drissi, D. and Mbekhta, M., Operators with bounded conjugation orbits Proc. Am. Math. Soc. 128 (2000), 2687–2691.CrossRefGoogle Scholar
8.Drissi, D. and Mbekhta, M., Elements with generalized bounded conjugation orbits Proc. Am. Math. Soc. 129 (2001), 2011–2016.CrossRefGoogle Scholar
9.Gelfand, I. M., Zur theorie der charactere der abelschen topologischen gruppen, Rec. Math. N. S. (Mat. Sb), 51 (1941), 49–50.Google Scholar
10.Gelfand, I., Raikov, D. and Shilov, G., Commutative normed rings (Chelsea Publ. Company, New York, 1964).Google Scholar
11.Gorin, E. A., Bernstein's inequality from the point of view of operator theory Selecta Math. Sov. 7 (1988), 191–209 (transl. from Vestnik Kharkov Univ. 45 (1980), 77–105).Google Scholar
12.Karaev, M. T. and Mustafayev, H. S., On some properties of Deddens algebras Rocky Mt. J. Math. 33 (2003), 915–926.CrossRefGoogle Scholar
13.Laursen, K. B. and Neuman, M., An introduction to the local spectral theory (Oxford, Clarendon Press, 2000).CrossRefGoogle Scholar
14.Levin, B. Ya., Distributions of zeros of entire functions, Amer. Math. Soc. Providence (1964).CrossRefGoogle Scholar
15.Lumer, G. and Rosenblum, M., Linear operators equations Proc. Am. Math. Soc. 10 (1959), 32–41.CrossRefGoogle Scholar
16.Roth, P. G., Bounded orbits of conjugation, analytic theory Indiana Univ. Math. J. 32 (1983), 491–509.CrossRefGoogle Scholar
17.Wermer, J., The existence of invariant subspaces Duke Math. J. 19 (1952), 615–622.CrossRefGoogle Scholar
18.Williams, J. P., On a boundedness condition for operators with a singleton spectrum, Proc. Am. Math. Soc. 78 (1980), 30–32.CrossRefGoogle Scholar