Article contents
GOLDIE*-SUPPLEMENTED MODULES
Published online by Cambridge University Press: 24 June 2010
Abstract
Motivated by a relation on submodules of a module used by both A. W. Goldie and P. F. Smith, we say submodules X, Y of M are β* equivalent, Xβ*Y, if and only if 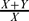 is small in
is small in 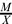 and
and 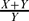 is small in
is small in 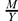 . We show that the β* relation is an equivalence relation and has good behaviour with respect to addition of submodules, homomorphisms and supplements. We apply these results to introduce the class of
. We show that the β* relation is an equivalence relation and has good behaviour with respect to addition of submodules, homomorphisms and supplements. We apply these results to introduce the class of 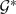 -supplemented modules and to investigate this class and the class of H-supplemented modules. These classes are located among various well-known classes of modules related to the class of lifting modules. Moreover these classes are used to explore an open question of S. H. Mohamed and B. J. Mueller. Examples are provided to illustrate and delimit the theory.
-supplemented modules and to investigate this class and the class of H-supplemented modules. These classes are located among various well-known classes of modules related to the class of lifting modules. Moreover these classes are used to explore an open question of S. H. Mohamed and B. J. Mueller. Examples are provided to illustrate and delimit the theory.
- Type
- Research Article
- Information
- Glasgow Mathematical Journal , Volume 52 , Issue A: Rings and Modules in Honour of Patrick F. Smith's 65th Birthday , July 2010 , pp. 41 - 52
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 2010
References
REFERENCES
- 15
- Cited by


