Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-24T13:06:07.688Z Has data issue: false hasContentIssue false
  • English
  • Français

GEOMETRIC INVARIANT THEORY FOR HOLOMORPHIC FOLIATIONS ON ℂℙ2 OF DEGREE 2

Published online by Cambridge University Press:  22 December 2010

CLAUDIA R. ALCÁNTARA
CLAUDIA R. ALCÁNTARA*
Affiliation:
Departamento de Matemáticas, Universidad de Guanajuato, Callejón Jalisco s/n, A.P. 402, C.P. 36000, Guanajuato, Gto. México; Université de Grenoble I, Département de Mathématiques, Institut Fourier. 38402 Saint-Martin d'Hères Cedex, France. e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 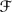2 be the space of the holomorphic foliations on ℂℙ2 of degree 2. In this paper we study the linear action PGL(3, ℂ) × 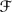2 → 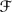2 given by gX = DgX ^(g−1) in the sense of the Geometric Invariant Theory. We obtain a characterisation of unstable and stable foliations according to properties of singular points and existence of invariant lines. We also prove that if X is an unstable foliation of degree 2, then X is transversal with respect to a rational fibration. Finally we prove that the geometric quotient of non-degenerate foliations without invariant lines is the moduli space of polarised del Pezzo surfaces of degree 2.

Keywords

Primary 37F7514L24
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 53 , Issue 1 , January 2011 , pp. 153 - 168
Copyright
Copyright © Glasgow Mathematical Journal Trust 2010

References

REFERENCES

1.Alcántara, C. R., Singular points and automorphisms of unstable foliations of ℂℙ, Boletín de la Sociedad Matemática Mexicana, to appear.Google Scholar
2.Brunella, M., Birational geometry of foliations, Lecture notes of the first Latin American Congress of Mathematicians (IMPA, Rio de Janeiro, Brazil, 2000).Google Scholar
3.Campillo, A. and Olivares, J., Polarity with respect to a foliation and Cayley-Bacharach Theorems,J. Reine Angew Math. 534 (2001), 95–118.Google Scholar
4.Cerveau, D., Déserti, J., Belko, D. Garba and Meziani, R., Géométrie classique des feuilletages quadratiques, arxiv:0902.0877.Google Scholar
5.Santos, W. F. and Rittatore, A., Actions and invariants of algebraic groups (Taylor and Francis, New York, NY, 2005).CrossRefGoogle Scholar
6.Fogarty, J., Kirwan, F. and Mumford, D., Geometric invariant theory (Springer-Verlag, Berlin, 1994).Google Scholar
7.Gómez-Mont, X. and Kempf, G., Stability of meromorphic vector fields in projective spaces, Comment. Math. Helvetici 64 (1989), 462–473.CrossRefGoogle Scholar
8.Gómez-Mont, X. and Ortiz-Bobadilla, L., Sistemas dinámicos holomorfos en superficies, in Aportaciones Matemáticas, Notas de Investigación, 3 (Sociedad Matemática Mexicana, México, 1989), 207.Google Scholar
9.Ishii, S., Moduli space of polarized del Pezzo surfaces and its compactification, Tokyo J. Math. 5 (1982), 289–297.CrossRefGoogle Scholar
10.Jouanolou, J. P., Equations de Pfaff Algébriques (Springer-Verlag, Berlin, 1979).CrossRefGoogle Scholar
11.Mendes, L. G., Kodaira dimension of holomorphic singular foliation, Bol. Soc. Bras. Mat. 31 (2000), 127–143.CrossRefGoogle Scholar
12.Neto, A. L. and Soares, M. G., Algebraic solutions of one-dimensional foliations, J. Differ. Geom. 43 (1996), 652–673.Google Scholar
13.Newstead, P., Introduction to moduli problems and orbit spaces (Springer-Verlag, Berlin, 1978).Google Scholar
14.Seidenberg, A., Reduction of singularities of the differential equation Ady = Bdx, Am. J. Math. 89 (1968), 248–269.CrossRefGoogle Scholar
15.Serre, J. P., Faisceaux algébriques cohérents, Ann. Math. 61 (1955), 197–278.CrossRefGoogle Scholar