Article contents
GENERALIZED HARDY–CESÀRO OPERATORS BETWEEN WEIGHTED SPACES
Published online by Cambridge University Press: 28 January 2018
Abstract
We characterize those non-negative, measurable functions ψ on [0, 1] and positive, continuous functions ω1 and ω2 on ℝ+ for which the generalized Hardy–Cesàro operator
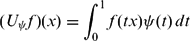 $$\begin{equation*}(U_{\psi}f)(x)=\int_0^1 f(tx)\psi(t)\,dt\end{equation*}$$
$$\begin{equation*}(U_{\psi}f)(x)=\int_0^1 f(tx)\psi(t)\,dt\end{equation*}$$
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 2018
References
REFERENCES
- 3
- Cited by


