Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-26T01:29:03.621Z Has data issue: false hasContentIssue false
  • English
  • Français

A functorial approach to weak amenability for commutative Banach algebras

Published online by Cambridge University Press:  18 May 2009

Volker Runde
Volker Runde
Affiliation:
Department of Mathematics, University of California, Berkeley, CA 94720, USA
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let A be a commutative algebra, and let M be a bimodule over A. A derivation from A into M is a linear mapping D: A→M that satisfies

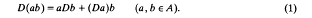
If M is only a left A-module, by a derivation from A into M we mean a linear mapping D: A→M such that

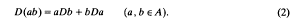
Each A-bimodule M is trivially a left module. However, unless it is commutative, i.e.

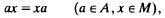
the two classes of linear operators from A into M characterized by (1) and (2), respectively, need not coincide.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 34 , Issue 2 , May 1992 , pp. 241 - 251
Copyright
Copyright © Glasgow Mathematical Journal Trust 1992

References

REFERENCES

1.Bade, W. G., Curtis, P. C. and Dales, H. G., Amenability and weak amenability for Beurling and Lipschitz algebras, Proc. London Math. Soc. (3) 55 (1987), 359–377.CrossRefGoogle Scholar
2.Bonsall, F. F. and Duncan, J., Complete normed algebras (Springer Verlag, 1973).CrossRefGoogle Scholar
3.Curtis, P. C. and Loy, R. J., The structure of amenable Banach algebras, London Math. Soc. (2) 40 (1989), 89–104.CrossRefGoogle Scholar
4.Grauert, H. and Remmert, R., Analytische Stellenalgebren (Springer Verlag, 1971).CrossRefGoogle Scholar
5.Grønbæk, N., Commutative Banach algebras, module derivations, and semigroups, London Math. Soc. (2) 40 (1989), 137–157.CrossRefGoogle Scholar
6.Grønbæk, N., A characterization of weakly amenable Banach algebras Studia Math. XCFV (1989), 149–162.CrossRefGoogle Scholar
7.Helemskiῐ, A. Ya., The homology of Banach and topological algebras, (Kluwer Academic Publishers, Dordrecht-Boston-London, 1989).CrossRefGoogle Scholar
8.Johnson, B. E., Cohomology in Banach algebras, Memoirs of the AMS 127 (1972).Google Scholar
9.Matsumura, H., Commutative algebra (W. A. Benjamin, New York, 1970).Google Scholar