Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-05T04:05:53.842Z Has data issue: false hasContentIssue false
  • English
  • Français

FRAME-LESS HILBERT C*-MODULES

Part of: Selfadjoint operator algebras Nontrigonometric harmonic analysis

Published online by Cambridge University Press:  07 February 2018

M. B. ASADI ,
M. FRANK Open the ORCID record for M. FRANK [Opens in a new window]  and
Z. HASSANPOUR-YAKHDANI
M. B. ASADI
Affiliation:
School of Mathematics, Statistics and Computer Science, College of Science, University of Tehran, Tehran, Iran School of Mathematics, Institute for Research in Fundamental Sciences (IPM), P.O. Box: 19395-5746, Tehran, Iran e-mail: [email protected]
M. FRANK
Affiliation:
Hochschule für Technik Wirtschaft und Kultur (HTWK) Leipzig, Fakultät IMN PF 301166, 04251 Leipzig, Germany e-mail: [email protected]
Z. HASSANPOUR-YAKHDANI
Affiliation:
School of Mathematics Statistics and Computer Science, College of Science, University of Tehran, Tehran, Iran e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that if A is a compact C*-algebra without identity that has a faithful *-representation in the C*-algebra of all compact operators on a separable Hilbert space and its multiplier algebra admits a minimal central projection p such that pA is infinite-dimensional, then there exists a Hilbert A1-module admitting no frames, where A1 is the unitization of A. In particular, there exists a frame-less Hilbert C*-module over the C*-algebra 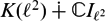$K(\ell^2) \dotplus \mathbb{C}I_{\ell^2}$.

MSC classification

Primary: 46L08: $C^*$-modules
Secondary: 42C15: General harmonic expansions, frames 46L05: General theory of $C^*$-algebras
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 61 , Issue 1 , January 2019 , pp. 25 - 31
Copyright
Copyright © Glasgow Mathematical Journal Trust 2018 

References

REFERENCES

1. Arambašić, Lj., Another characterization of Hilbert C*-modules over compact operators, J. Math. Anal. Appl. 344 (2) (2008), 735–740.Google Scholar
2. Amini, M., Asadi, M. B., Elliott, G. A. and Khosravi, F., Frames in Hilbert C*-modules and Morita equivalent C*-algebras, Glassgow Math. J. 59 (1) (2017), 1–10.Google Scholar
3. Arveson, W., An invitation to C*-algebras (Springer, New York, 1976).Google Scholar
4. Bakić, D. and Guljaš, B., Hilbert C*-modules over C*-algebras of compact operators, Acta Sci. Math. (Szeged) 68 (1–2) (2002), 249–269.Google Scholar
5. Brown, L. G., Complements to various Stone–Weierstrass theorems for C*-algebras and a theorem of Shultz, Comm. Math. Phys. 143 (2) (1992), 405–413.Google Scholar
6. Dixmier, J., C*-algebras (North-Holland Publishing Company, Amsterdam - New York - Oxford, 1977).Google Scholar
7. Elliott, G. A. and Kawamura, K., A Hilbert bundle characterization of Hilbert C*-modules, Trans. Amer. Math. Soc. 360 (9) (2008), 4841–4862.Google Scholar
8. Frank, M. and Larson, D. R., Frames in Hilbert C*-modules and C*-algebras, J. Operator Theory 48 (2) (2000), 273–314.Google Scholar
9. Li, H., A Hilbert C*-module admitting no frames, Bull. London Math. Soc. 42 (3) (2010), 388–394.Google Scholar
10. Swan, R. G., Vector bundles and projective modules, Trans. Amer. Math. Soc. 105 (2) (1962), 264–277.Google Scholar