Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-26T01:30:28.989Z Has data issue: false hasContentIssue false
  • English
  • Français

Existence de sous-espaces hyper-invariants

Published online by Cambridge University Press:  18 May 2009

K. Kellay
K. Kellay
Affiliation:
Universite Bordeaux I, Lamp, Ers0127, U.F.R. De Mathematiques Et Informatique, 351, Cours De La Liberation. 33405 Talence Cedex, France
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Soient B un espace de Banach et ℒ(B) l'algèbre des opérateurs bornés sur B. On dit qu'un sous-espace fermé E de B est invariant pour l'opérateur T ∈ ℒ(B) lorsque TE ⊂ E et qu'il est non trivial si {0} 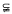E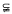B. Le sous-espace E est dit hyper-invariant pour T s'il est invariant pour tout opérateur qui commute avec T.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 40 , Issue 1 , March 1998 , pp. 133 - 141
Copyright
Copyright © Glasgow Mathematical Journal Trust 1998

References

REFERENCES

1.Allan, G. R. and Ransford, T. R., Power-dominated elements in Banach algebra, Studia Math., 94 (1989), 63–79.CrossRefGoogle Scholar
2.Atzmon, A., Operators which are annihilated by analytic functions and invariant subspaces, Acta Math., 144 (1980), 27–63.Google Scholar
3.Atzmon, A., On the existence of hyperinvariant subspaces, J. Operator Theory., 11 (1984), 3–40.Google Scholar
4.Beauzamy, B., Sous-espaces invariants de type fonctionnel dans les espaces de Banach, Acta Math., 144 (1980), 65–821.CrossRefGoogle Scholar
5.Beurling, A., Analytic continuation across a linear boundary, Acta Math., 128 (1972), 154–182.Google Scholar
6.Beurling, A. and Malliavin, P., The Fourier transforms of measures with compact support, Acta Math., 107 (1962), 291–309.CrossRefGoogle Scholar
7.Esterle, J., Quasimultipliers, representations of H”, and the closed ideal problem for commutative Banach algebras, Springer Led. Notes., 975 (1983), 66–162.Google Scholar
8.Helson, H., Boundedness from measure theory, linear operators and approximation, Proceedings of the conference held at Oberwolfach, 08 14–22, 1971, 129–137.CrossRefGoogle Scholar
9.Katznelson, Y., An introduction to harmonic analysis (Dover, New York, 1976).Google Scholar
10.Phong, V. Q., Semigroups with non quasianalytic growth, Studia Math., 96 (1993), 229–241.CrossRefGoogle Scholar
11.Wermer, J., The existence of invariant subspaces, Duke. Math. J., 19 (1952), 615–622.Google Scholar