Published online by Cambridge University Press: 25 July 2018
In this paper, we study the existence and concentration phenomena of solutions for the following non-local regional Schrödinger equation
where ϵ is a positive parameter, 0 < α < 1, 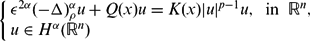 $$\begin{equation*}
\left\{
\begin{array}{l}
\epsilon^{2\alpha}(-\Delta)_\rho^{\alpha} u + Q(x)u = K(x)|u|^{p-1}u,\;\;\mbox{in}\;\; \mathbb{R}^n,\\
u\in H^{\alpha}(\mathbb{R}^n)
\end{array}
\right.
\end{equation*}$$
$$\begin{equation*}
\left\{
\begin{array}{l}
\epsilon^{2\alpha}(-\Delta)_\rho^{\alpha} u + Q(x)u = K(x)|u|^{p-1}u,\;\;\mbox{in}\;\; \mathbb{R}^n,\\
u\in H^{\alpha}(\mathbb{R}^n)
\end{array}
\right.
\end{equation*}$$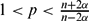 $1<p<\frac{n+2\alpha}{n-2\alpha}$, n > 2α; (−Δ)ρα is a variational version of the regional fractional Laplacian, whose range of scope is a ball with radius ρ(x) > 0, ρ, Q, K are competing functions.
$1<p<\frac{n+2\alpha}{n-2\alpha}$, n > 2α; (−Δ)ρα is a variational version of the regional fractional Laplacian, whose range of scope is a ball with radius ρ(x) > 0, ρ, Q, K are competing functions.