Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-26T07:57:48.907Z Has data issue: false hasContentIssue false
  • English
  • Français

EXISTENCE AND BIFURCATION RESULTS FOR FOURTH-ORDER ELLIPTIC EQUATIONS INVOLVING TWO CRITICAL SOBOLEV EXPONENTS

Published online by Cambridge University Press:  01 January 2009

D. A. KANDILAKIS ,
M. MAGIROPOULOS  and
N. ZOGRAPHOPOULOS
D. A. KANDILAKIS
Affiliation:
Department of Sciences, Technical University of Crete, 73100 Chania, Greece e-mail: [email protected]
M. MAGIROPOULOS
Affiliation:
Department of Sciences, Technological and Educational Institute of Crete, 71500 Heraklion, Greece e-mail: [email protected]
N. ZOGRAPHOPOULOS
Affiliation:
Department of Sciences, Technical University of Crete, 73100 Chania, Greece e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let Ω be a smooth bounded domain in RN, with N ≥ 5. We provide existence and bifurcation results for the elliptic fourth-order equation Δ2u − Δpu = f(λ, x, u) in Ω, under the Dirichlet boundary conditions u = 0 and ∇u = 0. Here λ is a positive real number, 1 < p ≤ 2# and f(.,., u) has a subcritical or a critical growth s, 1 < s ≤ 2*, where 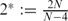and 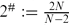. Our approach is variational, and it is based on the mountain-pass theorem, the Ekeland variational principle and the concentration-compactness principle.

Keywords

35J3535B3335G2035B32
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 51 , Issue 1 , January 2009 , pp. 127 - 141
Copyright
Copyright © Glasgow Mathematical Journal Trust 2008

References

REFERENCES

1.Brezis, H., Analyse fonctionnelle–Theorie et applications (Masson, Paris, 1983, 1993), (Dunod, Paris, 1999).Google Scholar
2.Brezis, H. and Nirenberg, L., Positive solutions of nonlinear elliptic equations involving critical Sobolev exponents, Commun. Pure Appl. Math. XXXVI (1983), 437–477.Google Scholar
3.Chabrowski, J., Drabek, P. and Tonkes, E., Asymptotic bifurcation results for quasilinear elliptic operators, Glasgow Math. J. 47 (2005), 55–67.CrossRefGoogle Scholar
4.Chabrowski, J. and doÓ, J. M., On some fourth-order semilinear elliptic problems in R N, Nonlin. Anal. TMA 49 (2002), 861–884.CrossRefGoogle Scholar
5.Chabrowski, J. and Yang, J., Nonnegative solutions for semilinear biharmonic equations in R N, Analysis 17 (1997), 35–59.Google Scholar
6. Q-Choi, H. and Jung, T., Positive solutions on nonlinear biharmonic equation, Kangweon-Kyungki Math. J. 5 (1) (1997), 29–33.Google Scholar
7.Drabek, P., Kufner, A. and Nicolosi, F., Quasilinear elliptic equations with degenerations and singularities (W. de Gruyter, Berlin, 1997).CrossRefGoogle Scholar
8.Edmunds, D. E., Fortunato, D. and Jannelli, E., Critical exponents, critical dimensions and the biharmonic operator, Arch. Rational Mech. Anal. 112 (1990), 269–289.Google Scholar
9.Ghoussoub, N., Duality and perturbation methods in critical point theory (Cambridge University Press, Cambridge, 1993).CrossRefGoogle Scholar
10.Grunau, H.-C. and Sweers, G., The maximum principle and positive principal eigenfunctions for polyharmonic equations, in Reaction-Diffusion Systems (Trieste, 1995), Lect. Notes Pure Appl. Math. 194 (Dekker, New York, 1998), 163–182).CrossRefGoogle Scholar
11.Guedda, M., On nonhomogeneous biharmonic equations involving critical Sobolev exponent, Portugaliae Math. 56 Fasc. 3 (1999), 299–308.Google Scholar
12.Jung, T. and Choi, Q-H., An application of a variational linking theorem to a non–linear biharmonic equation, Nonlinear Anal. TMA 47 (2001), 3695–3705.CrossRefGoogle Scholar
13.Lions, P. L., The concentration-compactness principle in the Calculus of Variations. The limit case, I, II. Rev. Mat. Iberoamer. 1 (1) (1985), 145–201 and 1(2) (1985), 45–121.CrossRefGoogle Scholar
14.Rabinowitz, P. H., Some global results for nonlinear eigenvalue problems, J. Funct. Anal. 7 (1971), 487–513.CrossRefGoogle Scholar
15.Van Der Vorst, R. C. A. M., Fourth order elliptic equations with critical growth, C. R. Acad. Sci. Paris Sér. I Math. 320 (3) (1995), 295–299.Google Scholar
16.Xu, G. and Zhang, J., Existence results for some fourth-order nonlinear elliptic problems of local superlinearity and sublinearity, J. Math. Anal. Appl. 281 (2003), 633–640.CrossRefGoogle Scholar