Published online by Cambridge University Press: 06 July 2018
For an orientable surface S of finite topological type with genus g ≥ 3, we construct a finite set of curves whose union of iterated rigid expansions is the curve graph 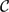 $\mathcal{C}$(S). The set constructed, and the method of rigid expansion, are closely related to Aramayona and Leiniger's finite rigid set in Aramayona and Leininger, J. Topology Anal.5(2) (2013), 183–203 and Aramayona and Leininger, Pac. J. Math.282(2) (2016), 257–283, and in fact a consequence of our proof is that Aramayona and Leininger's set also exhausts the curve graph via rigid expansions.
$\mathcal{C}$(S). The set constructed, and the method of rigid expansion, are closely related to Aramayona and Leiniger's finite rigid set in Aramayona and Leininger, J. Topology Anal.5(2) (2013), 183–203 and Aramayona and Leininger, Pac. J. Math.282(2) (2016), 257–283, and in fact a consequence of our proof is that Aramayona and Leininger's set also exhausts the curve graph via rigid expansions.