Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-22T20:15:07.975Z Has data issue: false hasContentIssue false
  • English
  • Français

Examples of malformed subsets of a Riemann surface

Published online by Cambridge University Press:  18 May 2009

Moses Glasner
Moses Glasner
Affiliation:
Pennsylvania State University, University Park, PA 16802, U.S.A.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let R be a hyperbolic Riemann surface and W an open subset of R with ∂W piecewise analytic. Denote by 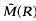the space of Dirichlet finite Tonelli functions on R and by π the harmonic projection of 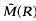. Consider the relative HD–class on W, HD(W;∂W) = {u∈ 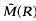│ u │ W∈HD(W) and u │ R\W = 0}. The extremization operation μ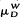is the linear mapping of HD(W;∂W) into HD(R) defined by μ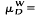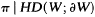. Since π preserves values of functions at the Royden harmonic boundary, the maximum principle implies that μ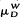is an order preserving injection and that Mμ 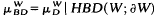is an isometry with respect to the supremum norms.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 24 , Issue 2 , July 1983 , pp. 101 - 106
Copyright
Copyright © Glasgow Mathematical Journal Trust 1983

References

REFERENCES

1.Nakai, M., Extremizations and Dirichlet integrals on Riemann surfaces, J. Math. Soc. Japan, 28 (1976), 581–603.CrossRefGoogle Scholar
2.Nakai, M., Malformed subregions of Riemann surfaces, J. Math. Soc. Japan, 29 (1977), 779–782.CrossRefGoogle Scholar
3.Nakai, M. and Segawa, S., Harmonic dimensions related to Dirichlet integrals, J. Math. Soc. Japan, 29 (1977), 107–121.CrossRefGoogle Scholar
4.Royden, H. L., Harmonic functions on open Riemann surfaces, Trans. Amer. Math. Soc. 73 (1952), 40–94.CrossRefGoogle Scholar
5.Sario, L. and Nakai, M., Classification theory of Riemann surfaces (Springer-Verlag, 1970).Google Scholar