Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-22T20:22:00.405Z Has data issue: false hasContentIssue false
  • English
  • Français

The evaluation functionals associated with an algebra of bounded operators

Published online by Cambridge University Press:  18 May 2009

J. Duncan
J. Duncan
Affiliation:
University of Aberdeen
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this note we shall employ the notation of [1] without further mention. Thus X denotes a normed space and P the subset of X × X′ given by

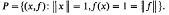
Given a subalgebra 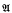of B(X), the set {Φ(X,f):(x,f) ∈ P} of evaluation functional on 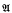is denoted by II. We shall prove that if X is a Banach space and if 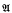contains all the bounded operators of finite rank, then Π is norm closed in 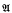′. We give an example to show that Π need not be weak* closed in 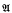″. We show also that FT need not be norm closed in 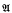″ if X is not complete.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 10 , Issue 1 , January 1969 , pp. 73 - 76
Copyright
Copyright © Glasgow Mathematical Journal Trust 1969

References

REFERENCES

1.Bonsall, F. F., The numerical range of an element of a normed algebra, Glasgow Math. J. 10 (1969), 68–72.CrossRefGoogle Scholar