Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-23T05:51:09.601Z Has data issue: false hasContentIssue false
  • English
  • Français

EMBEDDING MODULES OF FINITE HOMOLOGICAL DIMENSION

Published online by Cambridge University Press:  02 August 2012

SEAN SATHER-WAGSTAFF
SEAN SATHER-WAGSTAFF*
Affiliation:
Mathematics Department, NDSU, Dept #2750, PO Box 6050, Fargo, ND 58108-6050USA e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper builds on work of Hochster and Yao that provides nice embeddings for finitely generated modules of finite G-dimension, finite projective dimension or locally finite injective dimension. We extend these results by providing similar embeddings in the relative setting, that is, for certain modules of finite GC-dimension, finite 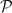C-projective dimension, locally finite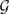 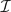C-injective dimension or locally finite 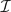C-injective dimension where C is a semidualizing module. Along the way, we extend some results for modules of finite homological dimension to modules of locally finite homological dimension in the relative setting.

Keywords

13D0213D0513D07
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 55 , Issue 1 , January 2013 , pp. 85 - 96
Copyright
Copyright © Glasgow Mathematical Journal Trust 2012

References

REFERENCES

1.Auslander, M., Anneaux de Gorenstein, et torsion en algèbre commutative, in Séminaire d'algèbre commutative dirigé par pierre samuel, vol. 1966/67 (Secrétariat mathématique, Paris, 1967), MR 37 #1435.Google Scholar
2.Auslander, M. and Bridger, M., Stable module theory, Memoirs of the American Mathematical Society, No. 94 (Amer. Math. Soc., Providence, RI, 1969), MR 42 #4580.CrossRefGoogle Scholar
3.Avramov, L. L. and Buchweitz, R.-O., Support varieties and cohomology over complete intersections, Invent. Math. 142 (2) (2000), 285–318. MR 1794064 (2001j:13017).Google Scholar
4.Avramov, L. L., Iyengar, S. B. and Lipman, J., Reflexivity and rigidity for complexes. I. Commutative rings, Algebra Number Theory 4 (1) (2010), 47–86. MR 2592013.CrossRefGoogle Scholar
5.Avramov, L. L. and Martsinkovsky, A., Absolute, relative, and Tate cohomology of modules of finite Gorenstein dimension, Proc. London Math. Soc. 85 (3) (2002), 393–440. MR 2003g:16009.Google Scholar
6.Christensen, L. W., Frankild, A. and Holm, H., On Gorenstein projective, injective and flat dimensions—A functorial description with applications, J. Algebra 302 (1) (2006), 231–279. MR 2236602.Google Scholar
7.Enochs, E. E. and Jenda, O. M. G., Gorenstein injective and projective modules, Math. Z. 220 (4) (1995), 611–633. MR 1363858 (97c:16011).Google Scholar
8.Enochs, E. E., Jenda, O. M. G. and Xu, J. Z., Foxby duality and Gorenstein injective and projective modules, Trans. Amer. Math. Soc. 348 (8) (1996), 3223–3234. MR 1355071 (96k:13010).Google Scholar
9.Foxby, H.-B., Gorenstein modules and related modules, Math. Scand. 31 (1972), 267–284. MR 48 #6094.CrossRefGoogle Scholar
10.Foxby, H.-B., Gorenstein dimensions over Cohen-Macaulay rings, in Proceedings of the international conference on commutative algebra (Bruns, W., Editor) (Universität Osnabrück, Osnabrück, Germany, 1994), 59–63.Google Scholar
11.Frankild, A. and Sather-Wagstaff, S., Reflexivity and ring homomorphisms of finite flat dimension, Commun. Algebra 35 (2) (2007), 461–500. MR 2294611.CrossRefGoogle Scholar
12.Golod, E. S., G-dimension and generalized perfect ideals, in Algebraic geometry and its applications, vol. 165 (Trudy Mat. Inst. Steklova, 1984), 62–66, MR 85m:13011.Google Scholar
13.Hartshorne, R., Residues and duality, Lecture Notes in Mathematics, vol. 20 (Springer-Verlag, Berlin, 1966). MR 36 #5145.CrossRefGoogle Scholar
14.Hochster, M. and Yao, Y., An embedding theorem for modules of finite (G-)projective dimension, preprint (2009).Google Scholar
15.Holm, H. and Jørgensen, P., Semidualizing modules and related Gorenstein homological dimensions, J. Pure Appl. Algebra 205 (2) (2006), 423–445. MR 2203625.Google Scholar
16.Holm, H. and White, D., Foxby equivalence over associative rings, J. Math. Kyoto Univ. 47 (4) (2007), 781–808. MR 2413065.Google Scholar
17.Sather-Wagstaff, S., Bass numbers and semidualizing complexes, in Commutative algebra and its applications (Walter de Gruyter, Berlin, 2009), 349–381. MR 2640315.Google Scholar
18.Sather-Wagstaff, S., Sharif, T. and White, D., Tate cohomology with respect to semidualizing modules, J. Algebra 324 (9) (2010), 2336–2368. MR 2684143.Google Scholar
19.Takahashi, R. and White, D., Homological aspects of semidualizing modules, Math. Scand. 106 (1) (2010), 5–22. MR 2603458.CrossRefGoogle Scholar
20.Vasconcelos, W. V., Divisor theory in module categories (North-Holland Publishing Co., Amsterdam, 1974), North-Holland Mathematics Studies, No. 14, Notas de Matemática No. 53. [Notes on Mathematics, No. 53]. MR 0498530 (58 #16637).Google Scholar
21.White, D., Gorenstein projective dimension with respect to a semidualizing module, J. Commut. Algebra 2 (1) (2010), 111–137. MR 2607104.Google Scholar