Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-22T01:25:02.235Z Has data issue: false hasContentIssue false
  • English
  • Français

Edge-realizable graphs with universal vertices

Published online by Cambridge University Press:  18 May 2009

Dalibor Fronček
Dalibor Fronček
Affiliation:
Department of Mathematics, Silesian University, Bezručovo Námestí 13, 74601 Opava, Czechoslovakia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

All graphs considered in this article are finite connected, without loops and multiple edges. Let G be a graph and x be a vertex. The vertex neighbourhood graph (or υ-neighbourhood) of x in G (denoted by 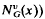is the subgraph of G induced by the set of all vertices of G adjacent to x Analogously if f = xy is any edge of G, the edge neighbourhood graph (or e-neighbourhood) of f in G is the subgraph of G (denoted 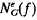or 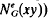induced by the set of all vertices of G which are adjacent to at least one vertex of the pair x, y and are different from x, y.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 33 , Issue 3 , September 1991 , pp. 309 - 310
Copyright
Copyright © Glasgow Mathematical Journal Trust 1991

References

REFERENCES

1.Fronček, D., Graphs with given edge neighbourhoods, Czech. Math. J. 39 (1989), 627–630.CrossRefGoogle Scholar
2.Fronček, D., Graphs with near v- and e-neighbourhoods, Glasgow Math. J. 42 (1990), 197–199.CrossRefGoogle Scholar
3.Harary, F., Graph theory (Addison–Wesley, 1969).CrossRefGoogle Scholar
4.Hell, P., Graphs with given neighborhoods I, Problèmes combinatoires et théorie des graphes, Colloque CNRS, 260, Orsay 1976, 219–223.Google Scholar
5.Nedela, R., Graphs which are edge-locally Cn, Czech. Math. J, to appear.Google Scholar
6.Zelinka, B., Edge neighbourhood graphs, Czech. Math. J. 36 (1986), 44–47.CrossRefGoogle Scholar
7.Zykov, A. A., Problem 30, in: Theory of graphs and its applications, Proc. Symp. Smolenice 1963 (Academia Prague, 1964), 164–165.Google Scholar