Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-26T16:19:58.421Z Has data issue: false hasContentIssue false
  • English
  • Français

Dunford-Pettis and strongly Dunford-Pettis operators on L1(μ)

Published online by Cambridge University Press:  18 May 2009

James R. Holub
James R. Holub
Affiliation:
Virginia Polytechnic Institute and State University, Blacksburg, Virginia 24061, USA.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Motivated by a problem in mathematical economics [4] Gretsky and Ostroy have shown [5] that every positive operator T:L1[0, 1] → c0 is a Dunford-Pettis operator (i.e. T maps weakly convergent sequences to norm convergent ones), and hence that the same is true for every regular operator from L1[0, 1] to c0. In a recent paper [6] we showed the converse also holds, thereby characterizing the D–P operators by this condition. In each case the proof depends (as do so many concerning D–P operators on Ll[0, 1]) on the following well-known result (see, e.g., [2]): If μ is a finite measure, an operator T:L1(μ) → E is a D–P operator 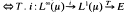is compact, where i:L∞(μ) → L1(μ) is the canonical injection of L∞(μ) into L1(μ). If μ is not a finite measure this characterization of D–P operators is no longer available, and hence results based on its use (e.g. [5], [6]) do not always have straightforward extensions to the case of operators on more general L1(μ) spaces.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 31 , Issue 1 , January 1989 , pp. 49 - 57
Copyright
Copyright © Glasgow Mathematical Journal Trust 1989

References

1.Banach, S., Theorie des Operationes Lineares, (Warsaw, 1933).Google Scholar
2.Bourgain, J., Dunford-Pettis operators on L 1 and the Radon-Nikodym property, Israel J. Math. 37 (1980), 34–47.CrossRefGoogle Scholar
3.Dunford, N. and Schwartz, J., Linear Operators I, (Interscience Publishers, 1963).Google Scholar
4.Gretsky, N. and Ostroy, J., Thick and thin market non-atomic exchange economies, Advances in Equilibrium Theory, Lecture notes in Economics and Mathematical Systems, 244 (1985), 107–130.Google Scholar
5.Gretsky, N. and Ostroy, J., The compact range property and c 0, Glasgow Math. J. 28 (1986), 113–114.CrossRefGoogle Scholar
6.Holub, J., A note on Dunford-Pettis operators, Glasgow Math. J. 29 (1987), 271–273.CrossRefGoogle Scholar
7.Rudin, W., Real and Complex Analysis (3rd Ed.), (McGraw-Hill Book Co., 1987).Google Scholar
8.Singer, I., Bases in Banach Spaces I, (Springer-Verlag, 1970).CrossRefGoogle Scholar