Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-17T17:06:47.783Z Has data issue: false hasContentIssue false
  • English
  • Français

DUALIZING INVOLUTIONS ON THE METAPLECTIC GL(2) à la TUPAN

Part of: Lie groups

Published online by Cambridge University Press:  10 July 2020

KUMAR BALASUBRAMANIAN  and
EKTA TIWARI
KUMAR BALASUBRAMANIAN
Affiliation:
Department of Mathematics, IISER Bhopal, Bhopal, Madhya Pradesh462066, India, e-mails: [email protected]; [email protected]
EKTA TIWARI
Affiliation:
Department of Mathematics, IISER Bhopal, Bhopal, Madhya Pradesh462066, India, e-mails: [email protected]; [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let F be a non-Archimedean local field of characteristic zero. Let G = GL(2, F) and 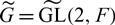$3\widetildeG = \widetilde{GL}(2,F)$ be the metaplectic group. Let τ be the standard involution on G. A well-known theorem of Gelfand and Kazhdan says that the standard involution takes any irreducible admissible representation of G to its contragredient. In such a case, we say that τ is a dualizing involution. In this paper, we make some modifications and adapt a topological argument of Tupan to the metaplectic group $\widetildeG$ and give an elementary proof that any lift of the standard involution to $\widetildeG$ ; is also a dualizing involution.

MSC classification

Primary: 22E50: Representations of Lie and linear algebraic groups over local fields
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 63 , Issue 2 , May 2021 , pp. 426 - 437
Copyright
© The Author(s), 2020. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Balasubramanian, K. and Bhand, A., Dualizing involutions on the metaplectc GL(2), accepted, DOI: 10.1016/j.jpaa.2020.106479.CrossRefGoogle Scholar
Gelbart, S. S., Weil’s representation and the spectrum of the metaplectic group, Lecture Notes in Mathematics, vol. 530 (Springer-Verlag, Berlin, New York, 1976). MR 0424695.CrossRefGoogle Scholar
Gelfand, I. M. and Kajdan, D. A., Representations of the group GL(n, K) where K is a local field, Lie groups and their representations Proc. Summer School, Bolyai János Math. Soc., Budapest, 1971 (Halsted, New York, 1975), 95–118. MR 0404534 (53 #8334).Google Scholar
Kable, A. C., The main involutions of the metaplectic group, Proc. Amer. Math. Soc. 127(4) (1999), 955–962. MR 1610921.Google Scholar
Kazhdan, D. A. and Patterson, S. J., Metaplectic forms, Inst. Hautes Études Sci. Publ. Math. 59 (1984), 35–142. MR 743816.CrossRefGoogle Scholar
Kazhdan, D. A. and Patterson, S. J., Towards a generalized Shimura correspondence, Adv. Math. 60(2) (1986), 161–234. MR 840303.Google Scholar
Kubota, T., On automorphic functions and the reciprocity law in a number field, Lectures in Mathematics, Department of Mathematics, Kyoto University, vol. 2 (Kinokuniya Book-Store Co., Ltd., Tokyo, 1969). MR 0255490.Google Scholar
Mackey, G. W., Les ensembles boréliens et les extensions des groupes, J. Math. Pures Appl. 36(9) (1957), 171–178. MR 0089998.Google Scholar
Serre, J.-P., A Course in Arithmetic (Springer-Verlag, New York, Heidelberg, 1973), Translated from the French, Graduate Texts in Mathematics, No. 7. MR 0344216.CrossRefGoogle Scholar
Tupan, A., A triangulation of GL(n, F), Represent. Theory 10 (2006), 158–163. MR 2219111.Google Scholar