Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-06T11:14:32.436Z Has data issue: false hasContentIssue false
  • English
  • Français

A Definition for Strong Rieszian Summability and its Relationship to Strong Cesaro Summability

Published online by Cambridge University Press:  18 May 2009

A. V. Boyd  and
J. M. Hyslop
A. V. Boyd
Affiliation:
University of the Witwatersrand, Johannesburg.
J. M. Hyslop
Affiliation:
University of the Witwatersrand, Johannesburg.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

1. Introduction. Given a series 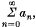we define 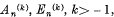, by the relations

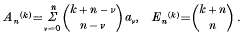
The series Σan is said to be summable (C, k) to the sum s, if

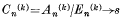
as n→∞, and strongly summable (C, k), k>0, with index p, to the sum s, or summable [C; k, p] to the sum s, if

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 1 , Issue 2 , July 1952 , pp. 94 - 99
Copyright
Copyright © Glasgow Mathematical Journal Trust 1952

References

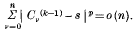
* Hyslop, J. M., Proc., Glasgow Math. Assoc., I., p. 16.Google Scholar

† See Lemma 2 below.

* Hardy, G. H. and Riesz, M., The General Theory of Dirichlet Series (Cambridge Tract, No. 18), 27.Google Scholar

† See, for example, Hyslop, J. M., Proc. Edinburgh Math. Soc., (2), 5 (1937), 46–54.CrossRefGoogle Scholar

‡ Kogbetliantz, E., Bull, des Sciences Math., (2), 49 (1925), 234–56.Google Scholar

§ Hyslop, J. M., loc. cit.Google Scholar

* Hardy, G. H. and Riesz, M., The General Theory of Dirichlet Series (Cambridge Tract, No. 18), 27.Google Scholar

† See, for example, Hyslop, J. M., Proc. Edinburgh Math. Soc., (2), 5 (1937), 46–54.CrossRefGoogle Scholar

‡ Kogbetliantz, E., Bull, des Sciences Math., (2), 49 (1925), 234–56.Google Scholar

§ Hyslop, J. M., loc. cit.Google Scholar

* Hobson, E. W., The Theory of Functions of a Real Variable, II (1926), 93.Google Scholar

* The term v = 0 in each of the preceding expressions is, of course, zero, and may therefore be omitted.