Published online by Cambridge University Press: 19 December 2014
A monoid S satisfies Condition (A) if every locally cyclic left S-act is cyclic. This condition first arose in Isbell's work on left perfect monoids, that is, monoids such that every left S-act has a projective cover. Isbell showed that S is left perfect if and only if every cyclic left S-act has a projective cover and Condition (A) holds. Fountain built on Isbell's work to show that S is left perfect if and only if it satisfies Condition (A) together with the descending chain condition on principal right ideals, MR. We note that a ring is left perfect (with an analogous definition) if and only if it satisfies MR. The appearance of Condition (A) in this context is, therefore, monoid specific. Condition (A) has a number of alternative characterisations, in particular, it is equivalent to the ascending chain condition on cyclic subacts of any left S-act. In spite of this, it remains somewhat esoteric. The first aim of this paper is to investigate the preservation of Condition (A) under basic semigroup-theoretic constructions. Recently, Khosravi, Ershad and Sedaghatjoo have shown that every left S-act has a strongly flat or Condition (P) cover if and only if every cyclic left S-act has such a cover and Condition (A) holds. Here we find a range of classes of S-acts 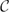 $\mathcal{C}$ such that every left S-act has a cover from
$\mathcal{C}$ such that every left S-act has a cover from 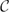 $\mathcal{C}$ if and only if every cyclic left S-act does and Condition (A) holds. In doing so we find a further characterisation of Condition (A) purely in terms of the existence of covers of a certain kind. Finally, we make some observations concerning left perfect monoids and investigate a class of monoids close to being left perfect, which we name left
$\mathcal{C}$ if and only if every cyclic left S-act does and Condition (A) holds. In doing so we find a further characterisation of Condition (A) purely in terms of the existence of covers of a certain kind. Finally, we make some observations concerning left perfect monoids and investigate a class of monoids close to being left perfect, which we name left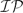 $\mathcal{IP}$a-perfect.
$\mathcal{IP}$a-perfect.