Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-04T17:42:57.226Z Has data issue: false hasContentIssue false
  • English
  • Français

A converse of an inequality of G. Bennett

Published online by Cambridge University Press:  18 May 2009

Horst Alzer
Horst Alzer
Affiliation:
Morsbacher Str. 105220 WaldbrölGermany
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove that if n>0 is an integer and r>0 is a real number, then

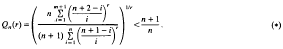
The upper bound is best possible. Inequality (*) is a converse of a result of G. Bennett who proved that Qn(r)>l.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 35 , Issue 2 , May 1993 , pp. 269 - 273
Copyright
Copyright © Glasgow Mathematical Journal Trust 1993

References

REFERENCES

1.Bennett, G., Some elementary inequalities, Quart. J. Math. Oxford (2), 38 (1987), 401–425.CrossRefGoogle Scholar
2.Bennett, G., Some elementary inequalities, II, Quart. J. Math. Oxford (2), 39 (1988), 385–400.CrossRefGoogle Scholar
3.Bennett, G., Some elementary inequalities, III, Quart. J. Math. Oxford (2), 42 (1991), 149–174.Google Scholar
4.Hardy, G. H., Littlewood, J. E. and Pólya, G., Inequalities, (Cambridge University Press, 1952).Google Scholar
5.König, H., Eigenvalue distribution of compact operators, (Birkhauser Verlag, Basel, 1986).CrossRefGoogle Scholar
6.Marshall, A. W. and Olkin, I., Inequalities: theory of majorization and its applications (Academic Press, 1979).Google Scholar