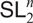Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
2020.
Editorial.
Glasgow Mathematical Journal,
Vol. 62,
Issue. S1,
p.
S1.
Beites, Patricia D.
Córdova-Martínez, Alejandra S.
Cunha, Isabel
and
Elduque, Alberto
2024.
Short $$(\textbf{SL}_2\times \textbf{SL}_2)$$-structures on Lie algebras.
Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas,
Vol. 118,
Issue. 2,