Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-26T17:54:00.591Z Has data issue: false hasContentIssue false
  • English
  • Français

CLUSTER AUTOMORPHISMS AND COMPATIBILITY OF CLUSTER VARIABLES

Published online by Cambridge University Press:  22 August 2014

IBRAHIM ASSEM ,
VASILISA SHRAMCHENKO  and
RALF SCHIFFLER
IBRAHIM ASSEM
Affiliation:
Département de mathématiques, Université de Sherbrooke, Sherbrooke, Qc, J1K 2R1, Canada e-mails: [email protected]; [email protected]
VASILISA SHRAMCHENKO
Affiliation:
Département de mathématiques, Université de Sherbrooke, Sherbrooke, Qc, J1K 2R1, Canada e-mails: [email protected]; [email protected]
RALF SCHIFFLER
Affiliation:
Department of Mathematics, University of Connecticut, Storrs, CT 06269-3009, USA e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we introduce a notion of unistructural cluster algebras, for which the set of cluster variables uniquely determines the clusters, as well as the notion of weak unistructural cluster algebras, for which the set of cluster variables determines the clusters, provided that the type of the cluster algebra is fixed. We prove that, for cluster algebras of the Dynkin type, the two notions of unistructural and weakly unistructural coincide, and that cluster algebras of rank 2 are always unistructural. We then prove that a cluster algebra 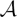$\mathcal A$ is weakly unistructural if and only if any automorphism of the ambient field, which restricts to a permutation of cluster variables of 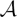$\mathcal A$, is a cluster automorphism. We also investigate the Fomin-Zelevinsky conjecture that two cluster variables are compatible if and only if one does not appear in the denominator of the Laurent expansions of the other.

Keywords

13F6016G20
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 56 , Issue 3 , September 2014 , pp. 705 - 720
Copyright
Copyright © Glasgow Mathematical Journal Trust 2014 

References

REFERENCES

1.Assem, I., Brüstle, T. and Schiffler, R., Cluster-tilted algebras and slices, J. Algebra 319 (2008), 3464–3479.CrossRefGoogle Scholar
2.Assem, I., Brüstle, T. and Schiffler, R., Cluster-tilted algebras without clusters, J. Algebra 324, (2010) 2475–2502.Google Scholar
3.Assem, I. and Dupont, G., Modules over cluster-tilted algebras determined by their dimension vectors. Comm. Algebra 41 (2) (2013), 4711–4721.Google Scholar
4.Assem, I., Schiffler, R. and Shramchenko, V., Cluster automorphisms, Proc. London Math. Soc. 3 (104) (2012), 1271–1302.Google Scholar
5.Assem, I., Simson, D. and Skowroński, A., Elements of the representation theory of associative algebras, 1: Techniques of representation theory, London Mathematical Society Student Texts, vol. 65 (Cambridge University Press, Cambridge, UK, 2006).Google Scholar
6.Buan, A. B. and Marsh, R., Denominators in cluster algebras of affine type, J. Algebra, 323 (8) (2010), 2083–2102.Google Scholar
7.Buan, A. B., Marsh, R., Reineke, M., Reiten, I. and Todorov, G., Tilting theory and cluster combinatorics, Adv. Math. 204 (2) (2006), 572–618.CrossRefGoogle Scholar
8.Buan, A. B., Marsh, R. and Reiten, I., Denominators of cluster variables, J. London Math. Soc. 79 (3) (2009), 589–611. doi: 10.1112/jlms/jdn082.CrossRefGoogle Scholar
9.Buan, A. B., Marsh, R. and Reiten, I., Cluster-tilted algebras, Trans. Amer. Math. Soc. 359 (1), (2007), 323–332.Google Scholar
10.Caldero, P. and Keller, B.. From triangulated categories to cluster algebras II. Ann. Sc. Ec. Norm. Sup. 39 (4) (2006), 83–100.Google Scholar
11.Fomin, S., Shapiro, M. and Thurston, D., Cluster algebras and triangulated surfaces. Part I: Cluster complexes, Acta Math. 201 (2008), 83–146.Google Scholar
12.Fomin, S. and Zelevinsky, A., Cluster algebras I. Foundations, J. Amer. Math. Soc. 15 (2) (2002), 497–529 (electronic).Google Scholar
13.Fomin, S. and Zelevinsky, A., Cluster algebras IV: Coefficients, Compos. Math. 143 (2007), 112–164.Google Scholar
14.Kimura, Y. and Qin, F., Graded quiver varieties, quantum cluster algebras, and dual canonical basis, arXiv:1205.2066v2.Google Scholar
15.Lee, K. and Schiffler, R., Positivity for cluster algebras, arXiv:1306.2415.Google Scholar
16.Lee, K. and Schiffler, R., A combinatorial algebra for rank 2 cluster variables, J. Algebra Comb. 37 (1), (2013), 67–85.Google Scholar
17.Musiker, G., Schiffler, R. and Williams, L., Positivity for cluster algebras from surfaces, Compos. Math. 149 (2) (2013), 217–263.CrossRefGoogle Scholar
18.Palu, Y., Cluster characters II: A multiplication formula, Proc. London Math. Soc. 104 (1) (2012), 57–78.CrossRefGoogle Scholar
19.Saleh, I., On the automorphisms of cluster algebras, arXiv: 1011.0894.Google Scholar