Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-23T01:50:33.497Z Has data issue: false hasContentIssue false
  • English
  • Français

CHARACTERIZATIONS OF STRICTLY SINGULAR AND STRICTLY COSINGULAR OPERATORS BY PERTURBATION CLASSES

Published online by Cambridge University Press:  02 August 2011

PIETRO AIENA ,
MANUEL GONZÁLEZ  and
ANTONIO MARTÍNEZ-ABEJÓN
PIETRO AIENA
Affiliation:
Dipartimento di Metodi e Modelli Matematici, Facoltà di Ingegneria, Università di Palermo, Viale delle Scienze, I-90128 Palermo, Italy E-mail: [email protected]
MANUEL GONZÁLEZ
Affiliation:
Departamento de Matemáticas, Facultad de Ciencias, Universidad de Cantabria, E-39071 Santander, Spain E-mail: [email protected]
ANTONIO MARTÍNEZ-ABEJÓN
Affiliation:
Departamento de Matemáticas, Facultad de Ciencias, Universidad de Oviedo, E-33007 Oviedo, Spain E-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider a class of operators that contains the strictly singular operators and it is contained in the perturbation class of the upper semi-Fredholm operators PΦ+. We show that this class is strictly contained in PΦ+, solving a question of Friedman. We obtain similar results for the strictly cosingular operators 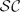and the perturbation class of the lower semi-Fredholm operators PΦ−. 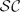We also characterize in terms of PΦ+ and in terms of PΦ−. As a consequence, we show that and 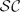are the biggest operator ideals contained in PΦ+ and PΦ−, respectively.

Keywords

47A53
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 54 , Issue 1 , January 2012 , pp. 87 - 96
Copyright
Copyright © Glasgow Mathematical Journal Trust 2011

References

REFERENCES

1.Aiena, P., Fredholm and local spectral theory, with application to multipliers (Kluwer, Dordrecht, 2004).Google Scholar
2.Aiena, P. and González, M., On inessential and improjective operators, Studia Math. 131 (1998), 271–287.Google Scholar
3.Aiena, P., González, M. and Martinón, A., On the perturbation classes of semi-Fredholm operators, Glasgow Math. J. 45 (2003), 91–95.CrossRefGoogle Scholar
4.Albiac, F. and Kalton, N., Topics in Banach space theory, Graduate Texts in Math., Vol. 233 (Springer, New York, 2006).Google Scholar
5.Avilés, A., Cabello, F., Castillo, J. M. F., González, M. and Moreno, Y., On separably injective Banach spaces. Preprint.Google Scholar
6.Castillo, J. M. F. and Plichko, A., Banach spaces in various positions, J. Funct. Anal. 259 (2010), 2098–2138.CrossRefGoogle Scholar
7.Friedman, T. L., Relating strictly singular operators to the condition X < Y mod() and resulting perturbations, Analysis (Munich) 22 (2002), 347–354.Google Scholar
8.Giménez, J., González, M. and Martí nez-Abejón, A., Perturbation of semi-Fredholm operators on products of Banach spaces, J. Operator Theory (to appear).Google Scholar
9.González, M., The perturbation classes problem in Fredholm theory, J. Funct. Anal. 200 (2003), 65–70.CrossRefGoogle Scholar
10.González, M. and Martí nez-Abejón, A., Tauberian operators, Operator Theory: Advances and Applications, Vol. 194 (Birkhäuser, Basel, 2010).CrossRefGoogle Scholar
11.González, M., Martí nez-Abejón, A. and Salas-Brown, M., Perturbation classes for semi-Fredholm operators on subprojective and superprojective spaces, Ann. Acad. Sci. Fennicae Math. (to appear).Google Scholar
12.González, M. and Salas-Brown, M., Perturbation classes for semi-Fredholm operators in L p(μ)-spaces, J. Math. Anal. Appl. 370 (2010), 11–17.CrossRefGoogle Scholar
13.Gowers, W. T. and Maurey, B., The unconditional basic sequence problem, J. Amer. Math. Soc. 6 (1993), 851–874.CrossRefGoogle Scholar
14.Kato, T., Perturbation theory for nullity, deficiency and other quantities of linear operators, J. d'Analyse Math. 6 (1958), 261–322.CrossRefGoogle Scholar
15.Pełczyński, A., On strictly singular and strictly cosingular operators I. Strictly singular and strictly cosingular operators in C(S)-spaces, Bull. Acad. Polon. Sci. 13 (1965), 31–36.Google Scholar
16.Pełczyński, A., On strictly singular and strictly cosingular operators II. Strictly singular and strictly cosingular operators in L(ν)-spaces, Bull. Acad. Polon. Sci. 13 (1965), 37–41.Google Scholar
17.Pietsch, A., Operator ideals (North-Holland, Amsterdam, 1980).Google Scholar
18.Taylor, A. E. and Lay, D. C., Introduction to functional analysis, 2nd ed. (Wiley, New York, 1980).Google Scholar
19.Vladimirskii, J. I., Strictly cosingular operators, Soviet Math. Doklady 8 (1967), 739–740.Google Scholar