Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-19T05:46:16.156Z Has data issue: false hasContentIssue false
  • English
  • Français

Centers of mass for operator-families

Published online by Cambridge University Press:  18 May 2009

Makoto Takaguchi
Makoto Takaguchi
Affiliation:
Department of Mathematics, Faculty of Science, Hirosaki University, Hirosaki 036, Japan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let Hbe a complex Hilbert space and let B(H) be the algebra of (bounded) operators on H. Let A =(A,…,An) be an n-tuple of operators on H. The joint numerical range of A is the subset W(A) of ℂn such that

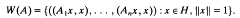
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 34 , Issue 1 , January 1992 , pp. 123 - 126
Copyright
Copyright © Glasgow Mathematical Journal Trust 1992

References

REFERENCES

1.Arveson, W., Subalgebras of C*-algebras II, Ada Math. 128 (1972), 271–308.Google Scholar
2.Chō, M. and Takaguchi, M., Some classes of commuting n-tuples of operators, Studia Math. 80 (1984), 245–259.CrossRefGoogle Scholar
3.Curto, R. E., Connections between Harte and Taylor spectra, Rev. Roumaine Math. Pares Appl. 31 (1986), 203–215.Google Scholar
4.Dekker, N. P., Joint numerical range and joint spectrum of Hilbert space operators (Ph.D. thesis, University of Amsterdam, 1969).Google Scholar
5.Stampfli, J. G., the norm of a derivation, Pacific J. Math. 33 (1970), 737–747.CrossRefGoogle Scholar
6.Takaguchi, M. and Chō, M., Joint normaloid operator-family, Sci. Rep. Hirosaki Univ. 27 (1980), 50–59.Google Scholar
7.Taylor, J. L., A joint spectrum for several commuting operators, J. Fund. Anal. 6 (1970), 172–191.CrossRefGoogle Scholar
8.Vasilescu, F.-H., A characterization of the joint spectrum in Hilbert spaces, Rev. Roumaine Math. Pures Appl. 22 (1977), 1003–1009.Google Scholar