No CrossRef data available.
Article contents
THE CASIMIR NUMBER AND THE DETERMINANT OF A FUSION CATEGORY
Published online by Cambridge University Press: 04 August 2020
Abstract
Let 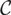 $\mathcal{C}$
be a fusion category over an algebraically closed field
$\mathcal{C}$
be a fusion category over an algebraically closed field 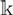 $\mathbb{k}$
of arbitrary characteristic. Two numerical invariants of
$\mathbb{k}$
of arbitrary characteristic. Two numerical invariants of 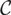 $\mathcal{C}$
, that is, the Casimir number and the determinant of
$\mathcal{C}$
, that is, the Casimir number and the determinant of 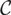 $\mathcal{C}$
are considered in this paper. These two numbers are both positive integers and admit the property that the Grothendieck algebra
$\mathcal{C}$
are considered in this paper. These two numbers are both positive integers and admit the property that the Grothendieck algebra 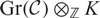 $(\mathcal{C})\otimes_{\mathbb{Z}}K$
over any field K is semisimple if and only if any of these numbers is not zero in K. This shows that these two numbers have the same prime factors. If moreover
$(\mathcal{C})\otimes_{\mathbb{Z}}K$
over any field K is semisimple if and only if any of these numbers is not zero in K. This shows that these two numbers have the same prime factors. If moreover 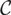 $\mathcal{C}$
is pivotal, it gives a numerical criterion that
$\mathcal{C}$
is pivotal, it gives a numerical criterion that 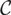 $\mathcal{C}$
is nondegenerate if and only if any of these numbers is not zero in
$\mathcal{C}$
is nondegenerate if and only if any of these numbers is not zero in 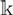 $\mathbb{k}$
. For the case that
$\mathbb{k}$
. For the case that 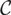 $\mathcal{C}$
is a spherical fusion category over the field
$\mathcal{C}$
is a spherical fusion category over the field 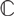 $\mathbb{C}$
of complex numbers, these two numbers and the Frobenius–Schur exponent of
$\mathbb{C}$
of complex numbers, these two numbers and the Frobenius–Schur exponent of 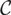 $\mathcal{C}$
share the same prime factors. This may be thought of as another version of the Cauchy theorem for spherical fusion categories.
$\mathcal{C}$
share the same prime factors. This may be thought of as another version of the Cauchy theorem for spherical fusion categories.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust


