Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-10T20:40:34.904Z Has data issue: false hasContentIssue false
  • English
  • Français

Capitulation in unramified quadratic extensions of real quadratic number fields

Published online by Cambridge University Press:  18 May 2009

E. Benjamin ,
F. Sanborn  and
C. Snyder
E. Benjamin
Affiliation:
Department of Mathematics, Unity College Unity, Maine 04988, USA
F. Sanborn
Affiliation:
Department of Mathematics, University of Maine, Orono, Maine 04469-5752, USA
C. Snyder
Affiliation:
Department of Mathematics, University of Maine, Orono, Maine 04469-5752, USA
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let k be an algebraic number field and Ck its ideal class group (in the wider sense). Suppose K is a finite extension of k. Then we say that an ideal class of k capitulates in K if this class is in the kernel of the homomorphism

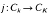
induced by extension of ideals from k to K (See Section 2 below). In [4], Iwasawa gives examples of real quadratic number fields, 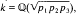with distinct primes Pi ≡ 1 (mod 4), for which all the ideal classes of the 2-class group, Ck,2 (the 2-Sylow subgroup of Ck), capitulate in an unramified quadratic extension of k. In these examples, Ck,2 is abelian of type (2,2), i.e. isomorphic to ℤ/2ℤ×ℤ/2ℤ and so all four ideal classes capitulate.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 36 , Issue 3 , September 1994 , pp. 385 - 392
Copyright
Copyright © Glasgow Mathematical Journal Trust 1994

References

REFERENCES

1.Cremona, J. E., and Odoni, R. W. K.. Some density results for negative Pell equations; an application of graph theory, J. London Math. Soc. (2) 39 (1989), 16–28.CrossRefGoogle Scholar
2.Cremona, J. E. and Odoni, R. W. K.. A generalization of a result of Iwasawa on the capitulation problem, Math. Proc. Cambridge Phil. Soc. 107 (1990), 1–3.CrossRefGoogle Scholar
3.Furtwängler, Ph., Über die Klassenzahl abelscher Zahlkörper, J. reine angew. Math. 134 (1908), 91–94.CrossRefGoogle Scholar
4.Iwasawa, K., A note on the capitulation problem for number fields, Proc. Japan Acad. Ser. A. Math. Sci. 65 (1989), 59–61.Google Scholar
5.Janusz, G., Algebraic Number Fields, (Academic Press, New York, London, 1973).Google Scholar
6.Kubota, T., Über den bizyklischen biquadratischen Zahlkörpern, Nagoya Math. J. 10 (1956), 65–85.CrossRefGoogle Scholar
7.Miyake, K., Algebraic investigations of Hilbert's Theorem 94, the principal ideal theorem, and the capitulation problem, Expo. Math. 7 (1989), 289–346.Google Scholar
8.Odoni, R. W. K., A note on a recent paper of Iwasawa on the capitulation problem, Proc. Japan Acad. Ser. A. Math. Sci. 65 (1989), 180–182.CrossRefGoogle Scholar
9.Rosen, M., Two theorems on Galois cohomology, Proc. Amer. Math. Soc. 17 (1966), 1183–1185.CrossRefGoogle Scholar