Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-26T17:17:55.357Z Has data issue: false hasContentIssue false
  • English
  • Français

Bounded completeness and Schauder's basis for C[0, 1]

Published online by Cambridge University Press:  18 May 2009

J. R. Holub
J. R. Holub
Affiliation:
Department of Mathematics, Virginia Polytechnic Institute and State University, Blacksburg, Virginia 24061, U.S.A.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A basis 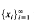, for a Banach space X is said to be boundedly complete [4, p. 284] if whenever 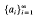is a sequence of scalars for which 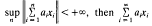converges. It is well-known [2, p. 70] that if 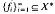is a boundedly complete basis for X then X is isometric to a conjugate space; in fact, X = [fi]*, where 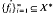is the sequence of coefficient functionals associated with the basis 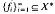It follows that no basis for C[0,1] can be boundedly complete since no separable conjugate space contains C0[l], yet C[0,1] is a separable space which contains c0.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 28 , Issue 1 , January 1986 , pp. 15 - 19
Copyright
Copyright © Glasgow Mathematical Journal Trust 1986

References

REFERENCES

1.Bessaga, C. and Pelczynski, A., On bases and unconditional convergence of series in Banach spaces, Studio Math. 17 (1958), 151–164.CrossRefGoogle Scholar
2.Day, M. M., Normed linear spaces (Springer-Verlag, 1962).CrossRefGoogle Scholar
3.Gohberg, I. and Krein, M., Introduction to the theory of linear nonselfadjoint operators, Translations of Mathematical Monographs, Volume 18 (American Mathematical Society, 1969).Google Scholar
4.Singer, I., Bases in Banach spaces I (Springer-Verlag, 1970).CrossRefGoogle Scholar