Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-26T17:16:42.633Z Has data issue: false hasContentIssue false
  • English
  • Français

Boundary value problems of singular elliptic partial differential equations

Published online by Cambridge University Press:  18 May 2009

Chi Yeung Lo
Chi Yeung Lo
Affiliation:
Michigan State University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In a recent paper [6], this author has extended the method of the kernel function [1] to the boundary value problems of the generalized axially symmetric potentials

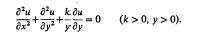
This method can also be applied to a more general class of singular differential equations, namely

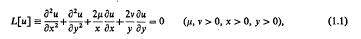
or, equivalently,

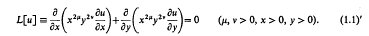
We shall derive in the sequel explicit formulas for the Dirichlet problems of (1.1) in the first quadrant of the x-y plane in terms of sufficiently smooth boundary data, and obtain an error-bound for their approximate solutions. We shall also indicate how the Neumann problem can be solved.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 13 , Issue 2 , September 1972 , pp. 111 - 118
Copyright
Copyright © Glasgow Mathematical Journal Trust 1972

References

REFERENCES

1.Bergman, S., The kernel function and conformal mapping, Amer. Math. Soc. Mathematical Surveys, No 5 (New York, 1950).Google Scholar
2.Bergman, S. and Herriot, J. G., Numerical solution of boundary value problems by the method of integral operator, Numer. Math. 7 (1965), 42–65.CrossRefGoogle Scholar
3.Erdélyi, A., Magnus, W., Oberhettinger, F. and Tricomi, F., Higher transcendental functions, Vols 1 and 2 (New York, 1955).Google Scholar
4.Gilbert, R. P., Integral operator methods in biaxially symmetric potential theory, Contributions to differential equations 2 (1963), 441–456.Google Scholar
5.Henrici, P., Complete systems of solutions for a class of singular partial differential equations, Boundary problems in differential equations (University of Wisconsin Press, 1960), 19–34.Google Scholar
6.Lo, C. Y., Boundary value problems of generalized axially symmetric potentials; to appear.Google Scholar
7.Natanson, I. P., Konstruktive Funktionentheorie (Berlin, 1955).Google Scholar
8.Szego, G., Orthogonal polynomials. Amer. Math. Soc. Colloquium Publications, Vol. 23 (Providence, R. I., 1967).Google Scholar
9.Watson, G. N., Notes on generating functions of polynomials (4). Jacobi polynomials, J. London Math. Soc. 9 (1934), 22–28.CrossRefGoogle Scholar