Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-19T06:27:57.476Z Has data issue: false hasContentIssue false
  • English
  • Français

BLOWUP FOR A DEGENERATE AND SINGULAR PARABOLIC EQUATION WITH NON-LOCAL SOURCE AND ABSORPTION*

Published online by Cambridge University Press:  25 November 2009

JUN ZHOU  and
CHUNLAI MU
JUN ZHOU
Affiliation:
School of mathematics and statistics, Southwest University, Chongqing 400715, China e-mail: [email protected]
CHUNLAI MU*
Affiliation:
College of mathematics and physics, Chongqing University, Chongqing 400044, China e-mail: [email protected]
*
†Corresponding author.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper deals with the following degenerate and singular equation 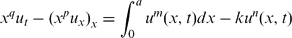with non-local source and absorption. The existence of a unique classical non-negative solution is established and the sufficient conditions for the solution that exists globally or blows up in finite time are obtained.

Keywords

35K5535K5735K65
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 52 , Issue 2 , May 2010 , pp. 209 - 225
Copyright
Copyright © Glasgow Mathematical Journal Trust 2009

Footnotes

*

The first author is supported by Natural Science Foundation Project of China SWU, SWU208029, the second author is supported by NNSF of China (10771226) and in part by Natural Science Foundation Project of CQ CSTC (2007BB0124).

References

REFERENCES

1.Andreucci, D. and DiBenedetto, E., A new approach to initial trace in nonlinear filtration, Annu. Inst. H. Poincar Anal. Non Linaire 7 (1990), 305–334.CrossRefGoogle Scholar
2.Budd, C., Galaktionov, V. A. and Chen, J., Focusing blow-up for quasilinear parabolic equations, Proc. R. Soc. Edinburgh Sec. A 128 (1998), 965–992.CrossRefGoogle Scholar
3.Chan, C. Y. and Chan, W. Y., Existence of classical solutions for degenerate semilinear parabolic problems, Appl. Math. Comput. 101 (1999), 125–149.Google Scholar
4.Chan, C. Y. and Liu, H. T., Global existence of solutions for degenerate semilinear parabolic problems, Nonlinear Anal. 34 (1998), 617–628.CrossRefGoogle Scholar
5.Chen, Y. P., Liu, Q. and Xie, C. H., Blow-up for degenerate parabolic equations with nonlocal source, Proc. Amer. Math. Soc. 132 (2004), 135–145.CrossRefGoogle Scholar
6.Chan, C. Y. and Yang, J., Complete blow-up for degenerate semilinear parabolic equations, J. Comput. Appl. Math. 113 (2000), 353–364.CrossRefGoogle Scholar
7.Chen, Y. P. and Xie, C. H., Blow-up for degenerate, singular, semilinear parabolic equations with nonlocal source, Acta Math. Sin. 47 (2004), 41–50.Google Scholar
8.Deng, W. B., Duan, Z. W. and Xie, C. H., The blow-up rate for a degenerate parabolic equation with a nonlocal source, J. Math. Anal. Appl. 264 (2001), 577–597.CrossRefGoogle Scholar
9.DiBenedetto, E., Degenerate parabolic equations (Springer-Verlag, New York, 1993).CrossRefGoogle Scholar
10.Dunford, N. and Schwartz, J. T., Linear operators. Part II: Spectral theory. Self adjoint operators in Hilbert space (JohnWiley & Sons, New York, 1963).Google Scholar
11.Floater, M. S., Blow-up at the boundary for degenerate semilinear parabolic equations, Arch. Rat. Mech. Anal. 114 (1991), 57–77.CrossRefGoogle Scholar
12.Friedman, A. and Mcleod, B., Blow-up of positive solutions of semilinear heat equations, India. Univ. Math. J. 34 (1985), 425–447.CrossRefGoogle Scholar
13.Galaktionov, V. A., Boundary values problems for the nonlinear parabolic equation ut = Δu σ+1 + up, Differentsial'nye Uravneniya 17 (1981), 836–842 (in Russian); English translation in Differ. Equ. 17 (1981), 551–555.Google Scholar
14.Ladyzenskaja, O. A., Solonik, V. A. and Ural'ceva, N. N., Linear and quasilinear equations of parabolic type, in Translations of mathematical monographs, vol. 23 (American Mathematical Society, Rhode Island, 1967).Google Scholar
15.Levine, H. A. and Sacks, P. E., Some existence and nonexistence theorems for solutions of degenerate parabolic equations, J. Differ. Equ. 52 (1984), 135–161.CrossRefGoogle Scholar
16.Li, J., Cui, Z. J. and Mu, C. L., Global existence and blow-up for degenerate and singular parabolic system with localized sources, Appl. Math. Comput. 199 (2008), 292–300.Google Scholar
17.Liu, Q. L., Chen, Y. P. and Xie, C. H., Blow-up for a degenerate parabolic equation with a nonlocal source, J. Math. Anal. Appl. 285 (2003), 487–505.CrossRefGoogle Scholar
18.Ockendon, H., Channel flow with temperature-dependent viscosity and internal viscous dissipation, J. Fluid Mech. 93 (1979), 737–746.CrossRefGoogle Scholar
19.Pao, C. V., Nonlinear parabolic and elliptic equations (Plenum Press, New York, 1992).Google Scholar
20.Peng, C. M. and Yang, Z. D., Blow-up for a degenerate parabolic equation with a nonlocal source, Appl. Math. Comput. 201 (2008), 250–259.Google Scholar
21.Sacks, P. E., Global behavior for a class of nonlinear evolutionary equations, SIAM J. Math. Anal. 16 (1985), 233–250.CrossRefGoogle Scholar
22.Samarskii, A. A., Galaktionov, V. A., Kurdyumov, S. P. and Mikhailoi, A. P., Blow-up in qusilinear parabolic equations (Nauka, Moscow, 1987).Google Scholar
23.Souplet, P., Uniform blow-up profiles and boundary behavior for diffusion equations with nonlocal nonlinear source, J. Differ. Equ. 153 (1999), 374–406.CrossRefGoogle Scholar
24.Wang, M. X. and Wang, Y. M., Properties of positive solutions for nonlocal reaction¤diffusion problems, Math. Methods Appl. Sci. 19 (1996), 1141–1156.3.0.CO;2-9>CrossRefGoogle Scholar
25.Zhou, J., Mu, C. L. and Li, Z. P., Blow up for degenerate and singular parabolic system with nonlocal source, Bound. Value Probl. 2006 (2006), 1–19.CrossRefGoogle Scholar