Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-23T15:22:00.803Z Has data issue: false hasContentIssue false
  • English
  • Français

Biduals of Banach spaces with bases

Published online by Cambridge University Press:  18 May 2009

Steven F. Bellenot
Steven F. Bellenot
Affiliation:
Department of Mathematics and Computer Science, The Florida State University, Tallahassee, Florida 32303, U.S.A.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

R. C. James [2] (or see p. 7ff of [3]) gave a useful representation of the bidual of any space with a shrinking basis. This note gives a representation of the bidual of any space with a basis.

Our notation follows that of [3], where undefined terms can be found. Let {en} be a basic sequence with coefficient functionals {fn}. We will assume {en} is bimonotone; that is

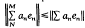. The space {en}LIM is the set of scalar sequences {an} so that ∥{an}∥ = 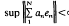. We will abuse notation and squate such {an} with the formal sum Σ anen.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 26 , Issue 1 , January 1985 , pp. 101 - 103
Copyright
Copyright © Glasgow Mathematical Journal Trust 1985

References

REFERENCES

1.Bellenot, S. F., The J-sum of Banach spaces, J. Functional Analysis 48 (1982), 95–106.CrossRefGoogle Scholar
2.James, R. C., Bases and reflexivity of Banach spaces, Ann. of Math. 52 (1950), 518–527.CrossRefGoogle Scholar
3.Lindenstrauss, J. and Tzafriri, L., Classical Banach spaces I Sequence Spaces (Springer Verlag, 1977).Google Scholar