Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-23T19:06:20.189Z Has data issue: false hasContentIssue false
  • English
  • Français

ASYMPTOTIC BEHAVIOR OF EIGENVALUES OF RECIPROCAL POWER LCM MATRICES

Published online by Cambridge University Press:  01 January 2008

SHAOFANG HONG  and
K. S. ENOCH LEE
SHAOFANG HONG*
Affiliation:
Mathematical College, Sichuan University, Chengdu 610064, P.R. China e-mail: [email protected]; [email protected]
K. S. ENOCH LEE
Affiliation:
Department of Mathematics, Auburn University Montgomery, Montgomery, AL 36124-4023, USA e-mail: [email protected]
*
The corresponding author is S. Hong who was supported by Program for New Century Excellent Talents in University Grant # NCET-06-0785 and by SRF for ROCS, SEM.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

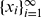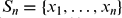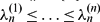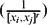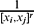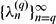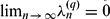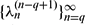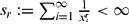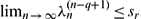Let be an arbitrary strictly increasing infinite sequence of positive integers. For an integer n≥1, let . Let r>0 be a real number and q≥ 1 a given integer. Let be the eigenvalues of the reciprocal power LCM matrix having the reciprocal power of the least common multiple of xi and xj as its i, j-entry. We show that the sequence converges and . We show that the sequence converges if and . We show also that if r> 1, then the sequence 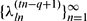converges and 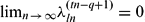, where t and l are given positive integers such that t≤l−1.

Keywords

Primary 11C2011A0515A36
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 50 , Issue 1 , January 2008 , pp. 163 - 174
Copyright
Copyright © Glasgow Mathematical Journal Trust 2008

References

REFERENCES

1.Altinisik, E., Sagan, B. E. and Tuglu, N., GCD matrices, posets, and nonintersecting paths, Linear Multilinear Algebra 53 (2005), 75–84.CrossRefGoogle Scholar
2.Apostol, T. M., Arithmetical properties of generalized Ramanujan sums, Pacific J. Math. 41 (1972), 281–293.CrossRefGoogle Scholar
3.Apostol, T. M., Introduction to analytic number theory (Springer-Verlag, 1976).CrossRefGoogle Scholar
4.Beslin, S. and Ligh, S., Greatest common divisor matrices, Linear Algebra Appl. 118 (1989), 69–76.CrossRefGoogle Scholar
5.Bourque, K. and Ligh, S., Matrices associated with arithmetical functions, Linear Multilinear Algebra 34 (1993), 261–267.CrossRefGoogle Scholar
6.Bourque, K. and Ligh, S., Matrices associated with classes of arithmetical functions, J. Number Theory 45 (1993), 367–376.CrossRefGoogle Scholar
7.Bourque, K. and Ligh, S., Matrices associated with classes of multiplicative functions, Linear Algebra Appl. 216 (1995), 267–275.CrossRefGoogle Scholar
8.Cao, W., On Hong's conjecture for power LCM matrices, Czechoslovak Math. J. 57 (2007), 253–268.CrossRefGoogle Scholar
9.Dickson, L. E., History of the theory of numbers, Vol. I (Chelsea Publ., 1999).Google Scholar
10.Hardy, G. H. and Wright, E. M., An introduction to the theory of numbers, Fourth Edition (Oxford University Press, 1960).Google Scholar
11.Haukkanen, P. and Korkee, I., Notes on the divisibility of LCM and GCD matrices, International J. Math. and Math. Science 6 (2005), 925–935.CrossRefGoogle Scholar
12.Haukkanen, P., Wang, J. and Sillanpää, J., On, Smith'sdetermiant, Linear Algebra Appl. 258 (1997), 251–269.CrossRefGoogle Scholar
13.Hedenmalm, H., Lindqvist, P. and Seip, K., A Hilbert space of Dirichlet series and systems of dilated functions in L 2(0, 1), Duke Math. J. 86 (1997), 1–37.CrossRefGoogle Scholar
14.Hilberdink, T., Determinants of multiplicative Toeplitz matrices, Acta Arith. 125 (2006), 265–284.CrossRefGoogle Scholar
15.Hong, S., Bounds for determinants of matrices associated with classes of arithmetical functions, Linear Algebra Appl. 281 (1998), 311–322.CrossRefGoogle Scholar
16.Hong, S., On the Bourque-Ligh conjecture of least common multiple matrices, J. Algebra 218 (1999), 216–228.CrossRefGoogle Scholar
17.Hong, S., Gcd-closed sets and determinants of matrices associated with arithmetical functions, Acta Arith. 101 (2002), 321–332.CrossRefGoogle Scholar
18.Hong, S., On the factorization of LCM matrices on gcd-closed sets, Linear Algebra Appl. 345 (2002), 225–233.CrossRefGoogle Scholar
19.Hong, S., Factorization of matrices associated with classes of arithmetical functions, Colloq. Math. 98 (2003), 113–123.CrossRefGoogle Scholar
20.Hong, S., Notes on power LCM matrices, Acta Arith. 111 (2004), 165–177.CrossRefGoogle Scholar
21.Hong, S., Nonsingularity of matrices associated with classes of arithmetical functions, J. Algebra 281 (2004), 1–14.CrossRefGoogle Scholar
22.Hong, S., Nonsingularity of least common multiple matrices on gcd-closed sets, J. Number Theory 113 (2005), 1–9.CrossRefGoogle Scholar
23.Hong, S., Nonsingularity of matrices associated with classes of arithmetical functions on lcm-closed sets, Linear Algebra Appl. 416 (2006), 124–134.CrossRefGoogle Scholar
24.Hong, S. and Loewy, R., Asymptotic behavior of eigenvalues of greatest common divisor matrices, Glasgow Math. J. 46 (2004), 551–569.CrossRefGoogle Scholar
25.Hong, S. and Loewy, R., Asymptotic behavior of the smallest eigenvalue of matrices associated with completely even functions (mod r), submitted.Google Scholar
26.Hong, S., Shum, K. P. and Sun, Q., On nonsingular power LCM matrices, Algebra Colloq. 13 (2006), 689–704.CrossRefGoogle Scholar
27.Horn, R. and Johnson, C. R., Matrix analysis (Cambridge University Press, 1985).CrossRefGoogle Scholar
28.Hwang, S., Cauchy's interlace theorem for eigenvalues of Hermitian matrices, Amer. Math. Monthly 111 (2004), 157–159.CrossRefGoogle Scholar
29.Korkee, I. and Haukkanen, P., On meet and join matrices associated with incidence functions, Linear Algebra Appl. 372 (2003), 127–153.CrossRefGoogle Scholar
30.Li, M., Notes on Hong's conjectures of real number power LCM matrices, J. Algebra 315 (2007), 654–664.CrossRefGoogle Scholar
31.Lindqvist, P. and Seip, K., Note on some greatest common divisor matrices, Acta Arith. 84 (1998), 149–154.CrossRefGoogle Scholar
32.McCarthy, P. J., A generalization of Smith's determinant, Canad. Math. Bull. 29 (1986), 109–113.CrossRefGoogle Scholar
33.Niven, I. and Zuckerman, H., An introduction to the theory of numbers, Third Edition (Wiley, New York, 1960).Google Scholar
34.Sándor, J. and Crstici, B., Handbook of number theory II (Kluwer Academic Publishers, 2004).CrossRefGoogle Scholar
35.Smith, H. J. S., On the value of a certain arithmetical determinant, Proc. London Math. Soc. 7 (1875–1876), 208–212.CrossRefGoogle Scholar
36.Wintner, A., Diophantine approximations and Hilbert's space, Amer. J. Math. 66 (1944), 564–578.CrossRefGoogle Scholar
37.Zhao, J., Hong, S., Liao, Q. and Shum, K. P., On the divisibility of power LCM matrices by power GCD matrices, Czechoslovak Math. J. 57 (2007), 115–125.CrossRefGoogle Scholar