Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-26T14:15:02.411Z Has data issue: false hasContentIssue false
  • English
  • Français

Arithmetical Functions of a Greatest Common Divisor, III. Cesàro's Divisor Problem

Published online by Cambridge University Press:  18 May 2009

Eckford Cohen
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let σ1(n) denote the sum of the tth powers of the divisors of n, σ(n) = σ1(n). Also place

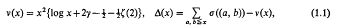
where γ is Euler's constant, ζ(s) is the Riemann ζ-function and x ≧ 2. The function Δ(x) is the remainder term arising in the divisor problem for σ((m, n)). Cesàro proved originally [1], [6, p. 328] that Δ(x) = o(x2 log x). More recently in I [2, (3.14)] it was shown by elementary methods that 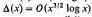. This estimate was later improved to 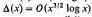in II [3, (3.7)]. In the present paper (§ 3) we obtain a much more substantial reduction in the order of Δ(x), by showing that Δ(x) can be expressed in terms of the remainder term in the classical Dirichlet divisor problem. On the basis of well known results for this problem, it follows easily that 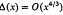. The precise statement of the result for σ((m, n)) is contained in (3.2).

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 5 , Issue 2 , July 1961 , pp. 67 - 75
Copyright
Copyright © Glasgow Mathematical Journal Trust 1961

References

1.Cesàro, Ernest, Étude moyenne du plus grand commun diviseur de deux nombres, Annali di Matematica Pura ed Applicata (2), 13 (1885), 233–268.Google Scholar
2.Cohen, Eckford, Arithmetical functions of a greatest common divisor. I, Proc. American Math. Soc., 11 (1960), 164–171.Google Scholar
3.Cohen, Eckford, Arithmetical functions of a greatest common divisor, II. Submitted to Boll. Mat. Ital.Google Scholar
4.Corput, J. G. van der, Zum Teilerproblem, Math. Ann. 98 (1928), 697–716.CrossRefGoogle Scholar
5.Davenport, H., A divisor problem, Quart. J. Math. Oxford Ser. (2), 20 (1949), 37–44.CrossRefGoogle Scholar
6.Dickson, L. E., History of the theory of numbers (New York, 1952), vol. I.Google Scholar
7.Ingham, A. E., The distribution of prime numbers (Cambridge, 1932).Google Scholar
8.Landau, Edmund, Über Dirichlets Teilerproblem, Göttinger Nachr. (1920), 13–32.Google Scholar
9.Landau, Edmund, Vorlesungen über Zahlentheorie (New York, 1957), vol. II.Google Scholar