Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-01-11T03:22:42.909Z Has data issue: false hasContentIssue false
  • English
  • Français

AN INTERTWINING OPERATOR FOR THE GROUP B 2

Published online by Cambridge University Press:  09 August 2007

CHARLES F. DUNKL
CHARLES F. DUNKL*
Affiliation:
Department of Mathematics, PO Box 400137, University of Virginia, Charlottesville, VA 22904-4137 e-mail: [email protected] URL: http://www.people.virginia.edu/~cfd5z/
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

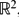There is a commutative algebra of differential-difference operators, acting on polynomials on , associated with the reflection group B 2. This paper presents an integral transform which intertwines this algebra, allowing one free parameter, with the algebra of partial derivatives. The method of proof depends on properties of a certain class of balanced terminating hypergeometric series of 4 F 3-type. These properties are in the form of recurrence and contiguity relations and are proved herein.

Keywords

Primary 33C8033C20Secondary 33C7043A80
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 49 , Issue 2 , May 2007 , pp. 291 - 319
Copyright
Copyright © Glasgow Mathematical Journal Trust 2007

References

REFERENCES

1. Bailey, W., Generalized hypergeometric series (Cambridge University Press 1935).Google Scholar
2. Dunkl, C., Differential-difference operators associated to reflection groups, Trans. Amer. Math. Soc. 311 (1989), 167–183.CrossRefGoogle Scholar
3. Dunkl, C., Operators commuting with Coxeter group actions on polynomials, in Invariant theory and tableaux (Stanton, D., ed.), (Springer-Verlag, 1990), 107–117.Google Scholar
4. Dunkl, C., Intertwining operators associated to the group S3, Trans. Amer. Math. Soc. 347 (1995), 3347–3374.Google Scholar
5. Dunkl, C., de Jeu, M., and Opdam, E., Singular polynomials for finite reflection groups, Trans. Amer. Math. Soc. 346 (1994), 237–256.CrossRefGoogle Scholar
6. Dunkl, C. and Xu, Y., Orthogonal polynomials of several variables, Encyclopaedia of Mathematics and its Applications 81 (Cambridge University Press, 2001).Google Scholar
7. Helgason, S., Groups and geometric analysis (Academic Press, New York, 1984).Google Scholar
8. Rösler, M., Positivity of Dunkl's intertwining operator, Duke Math. J. 98 (1999), 445–463.CrossRefGoogle Scholar
9. Rösler, M., Dunkl operators: theory and applications, Orthogonal polynomials and special functions (Leuven 2002), (Koelink, E. and Assche, W. Van, eds.), (Springer-Verlag, 2003), 93–135.CrossRefGoogle Scholar
10. Xu, Y., A product formula for Jacobi polynomials, Special functions (Hong Kong 1999), (Dunkl, C., Ismail, M., Wong, R., eds.), (World Scientific, Singapore, 2000), 423–430.CrossRefGoogle Scholar