Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-26T08:02:56.374Z Has data issue: false hasContentIssue false
  • English
  • Français

An infinitesimal proof of the implicit function theorem

Published online by Cambridge University Press:  18 May 2009

Nigel J. Cutland  and
Feng Hanqiao
Nigel J. Cutland
Affiliation:
Department of Pure MathematicsUniversity of HullHull HU6 7RXEngland
Feng Hanqiao
Affiliation:
Department of Computer ScienceShaanxi UniversityXian, 710062China
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We give a short and constructive proof of the general (multi-dimensional) Implicit Function Theorem (IFT), using infinitesimal (i.e. nonstandard) methods to implement our basic intuition about the result. Here is the statement of the IFT, quoted from [4];

Theorem. Let A ⊂ ℝn × ℝmbe an open set and let F:A → ℝ be a function of class Cp (p≥1). Suppose that (xO, yO) ε A with F(xO, yO) = 0 (xO ε ℝn, yO ε ℝm) and that the Jacobian determinant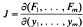is not zero at (xO, yO). Then there is an open neighbourhood U of xO and a unique function f:U→ ℝmwith

F(x, f(x)) = 0

for all x ε U. Moreover, f is of class Cp.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 35 , Issue 2 , May 1993 , pp. 163 - 166
Copyright
Copyright © Glasgow Mathematical Journal Trust 1993

References

REFERENCES

1.Cutland, N. J., (Editor), Nonstandard analysis and its applications (Cambridge University Press, 1988).CrossRefGoogle Scholar
2.Feng Hanqiao, D. F., Mary, St. and Wattenberg, F., Applications of nonstandard analysis to partial differential equations—the diffusion equation, Mathematical Modelling, 7 (1986) 507–523.Google Scholar
3.Hurd, A. E. and Loeb, P. A., An introduction to nonstandard real analysis (Academic Press, 1985).Google Scholar
4.Marsden, J. E., Elementary classical analysis (W. H. Freeman, 1974).Google Scholar