Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ratti, J. S.
1967.
Tauberian theorems for absolute summability.
Proceedings of the American Mathematical Society,
Vol. 18,
Issue. 5,
p.
775.
Ratti, J. S.
1969.
On a relation between absolute Abel and absolute Riesz summability..
Proceedings of the American Mathematical Society,
Vol. 21,
Issue. 1,
p.
57.
Okutoyi, J. I.
1990.
On the spectrum of C1 as an operator on bv0.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 48,
Issue. 1,
p.
79.


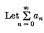 be a given series and let
be a given series and let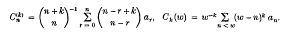
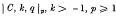 , q real, if
, q real, if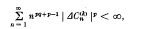
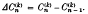 Summability |
Summability |