Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-26T07:17:33.628Z Has data issue: false hasContentIssue false
  • English
  • Français

Addendum to a paper of M. Saks

Published online by Cambridge University Press:  18 May 2009

Hazel Perfect
Hazel Perfect
Affiliation:
University of Sheffield
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Throughout, (X, ≤ ) denotes a partially ordered set (p. o. set), where X is assumed to be finite. A subset Y of X is called a k-union if Y contains no chain of length K + 1. In particular, therefore, a 1-union is just an antichain; and it is readily seen that Y is a k-union if and only if it is a union of K antichains. (Dually, a subset Z of X is a k-counion if Z contains no antichain of length k + 1.) We denote by dk (X) the maximum cardinality of a k-union in X, with a similar notation for other p. o. sets. Now let 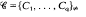be any partition of X into chains, and write

.

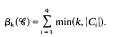Type
Research Article
Information
Glasgow Mathematical Journal , Volume 25 , Issue 1 , January 1984 , pp. 31 - 33
Copyright
Copyright © Glasgow Mathematical Journal Trust 1984

References

REFERENCES

1.Dilworth, R. P., A decomposition theorem for partially ordered sets, Ann. of Math. 51 (1950), 161–166.CrossRefGoogle Scholar
2.Freese, R., An application of Dilworth's lattice of maximal antichains, Discrete Math. 7 (1974), 107–109.CrossRefGoogle Scholar
3.Greene, C. and Kleitman, D. J., The structure of Sperner k-families, J. Combin. Theory Ser. A 20 (1976), 41–68.CrossRefGoogle Scholar
4.Saks, M., A short proof of the existence of k-saturated partitions of partially ordered sets, Adv. in Math. 33 (1979), 207–211.CrossRefGoogle Scholar