Hostname: page-component-6bf8c574d5-t27h7 Total loading time: 0 Render date: 2025-02-28T16:21:00.721Z Has data issue: false hasContentIssue false
  • English
  • Français

Theory of heat equations for sigma functions

Part of: Abelian varieties and schemes Other special functions Arithmetic algebraic geometry Curves

Published online by Cambridge University Press:  28 February 2025

J. Chris Eilbeck Open the ORCID record for J. Chris Eilbeck [Opens in a new window] ,
John Gibbons ,
Yoshihiro Ônishi  and
Seidai Yasuda
J. Chris Eilbeck*
Affiliation:
Department of Mathematics and the Maxwell Institute for Mathematical Sciences Heriot-Watt University, Edinburgh, UK
John Gibbons
Affiliation:
Department of Mathematics, Imperial College, London, UK
Yoshihiro Ônishi
Affiliation:
Department of Mathematics, Faculty of Science and Technology Meijo University, Tenpaku, Nagoya, Japan
Seidai Yasuda
Affiliation:
Department of Mathematics, Hokkaido University, Sapporo, Japan
*
Corresponding author: J. Chris Eilbeck; Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let $e$ and 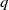$q$ be fixed co-prime integers satisfying 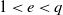$1\lt e\lt q$. Let 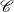$\mathscr {C}$ be a certain family of deformations of the curve 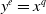$y^e=x^q$. That family is called the 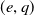$(e,q)$-curve and is one of the types of curves called plane telescopic curves. Let $\varDelta$ be the discriminant of 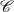$\mathscr {C}$. Following pioneering work by Buchstaber and Leykin (BL), we determine the canonical basis 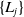$\{ L_j \}$ of the space of derivations tangent to the variety 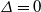$\varDelta =0$ and describe their specific properties. Such a set 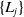$\{ L_j \}$ gives rise to a system of linear partial differential equations (heat equations) satisfied by the function 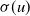$\sigma (u)$ associated with 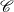$\mathscr {C}$, and eventually gives its explicit power series expansion. This is a natural generalisation of Weierstrass’ result on his sigma function. We attempt to give an accessible description of various aspects of the BL theory. Especially, the text contains detailed proofs for several useful formulae and known facts since we know of no works which include their proofs.

Keywords

Weierstrass sigma functionelliptic functionsheat equations

MSC classification

Primary: 33E99: None of the above, but in this section 14K25: Theta functions 14H42: Theta functions; Schottky problem
Secondary: 11G05: Elliptic curves over global fields
Type
Research Article
Information
Glasgow Mathematical Journal , First View , pp. 1 - 58
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

*

Version : December 7, 2024

References

Arnol’d, V. I., Wave front evolution and equivariant Morse lemma, Comm. Pure and Appl. Math XXIX (1976), 557–582.CrossRefGoogle Scholar
Arnol’d, V. I., Singularities of caustics and wave fronts, Mathematics and its Applications, vol. 62 (Kluwer, 1990).Google Scholar
Bernatska, J., General derivative Thomae formula for singular half-periods, Lett. Math. Phys. 110(11) (2020), 2983–3014.CrossRefGoogle Scholar
Bernatska, J., New generalisation of Jacobi’s derivative formula, Ramanujan J. 58(2) (2022), 319–368.CrossRefGoogle Scholar
Bruce, J. W., Functions on discriminants, J. London Math. Soc. 30(2) (1984), 551–567.CrossRefGoogle Scholar
Buchstaber, V. M. and Leykin, D. V., Polynomial Lie Algebras, Funct. Anal. Appl. 36(4) (2002), 267–280.CrossRefGoogle Scholar
Buchstaber, V. M. and Leykin, D. V., Heat equations in a nonholonomic frame, Functional Anal. Appl. 38 (2004), 88–101.CrossRefGoogle Scholar
Buchstaber, V. M. and Leykin, D. V., Addition laws on Jacobian varieties of plane algebraic curves, in Proceedings of The Steklov Institute of Mathematics, vol. 251 (2005), 1–72.Google Scholar
Buchstaber, V. M. and Leykin, D. V., Solution of the problem of differentiation of Abelian functions over parameters for families of -curves, Funct. Anal. Appl. 42 (2008), 268–278.CrossRefGoogle Scholar
Buchstaber, V. M., Enolskii, V. Z. and Leykin, D. V., Kleinian functions, hyperelliptic Jacobians and applications, J. Math. Phys. 10 (1997), 1–125.Google Scholar
Chevalley, C. (1951). Introduction to the theory of algebraic functions of one variable, Mathematical Surveys, VI (A.M.S., Providence, RI, 1951).Google Scholar
Eilbeck, J. C. and Ônishi, Y., Recursion relations on the power series expansion of the universal Weierstrass sigma function, RIMS Kôkyûroku Bessatsu 78 (2020), 77–98.Google Scholar
Eilbeck, J. C., Enol’skii, V. Z., Matsutani, S., Ônishi, Y. and Previato, E., Abelian functions for trigonal curves of genus three, Int Math Res Notices 2007 (2007), 102–139.Google Scholar
Frobenius, G. F. and Stickelberger, L., Ueber die differentiation der elliptischen functionen nach den perioden und invarianten, J. Reine Angew. Math. 92 (1882), 311–327.Google Scholar
Gelfand, I. M., Kapranov, M. M. and Zelevinsky, A. V., Discriminants, resultants, and multidimensional determinants, (Birkhäuser, 1994).CrossRefGoogle Scholar
Grant, D., A generalization of Jacobi’s derivative formula to dimension two, J. Reine Angew. Math 392(1988), 125–136.Google Scholar
Lang, S., An introduction to algebraic and Abelian functions, 2nd Edition, (Springer-Verlag, 1982).CrossRefGoogle Scholar
Lewittes, J., Rieman surfaces and the theta function, Acta Math. 111(1964), 37–61.CrossRefGoogle Scholar
Manin, Ju. I., Algebraic curves over fields with differentiation 1964, A. M. S. Transl., Twenty two papers on algebra, number theory and differential geometry 37 (1964), 59–78.Google Scholar
Matsumura, H., Commutative ring theory, Cambridge studies advanced mathematics, vol. 8, (Cambridge University Press, 1980).Google Scholar
Miura, S., Linear codes on affine algebraic curves (in Japanese, Affine dai-su-kyoku-sen-zyo no sen-kei-fu-gou), J. IEICE A. 81 (1998), 1398–1421.Google Scholar
Mumford, D., Tata lectures on theta II, Progress in Mathematics, vol. 43 (Birkhäuser, 1984).Google Scholar
Nakayashiki, A., On algebraic expressions of sigma functions for $(n,s)$ curves, Asian J. Math. 14(2) (2010), 175–212.CrossRefGoogle Scholar
Nakayashiki, A., Sigma function as a tau function, Int. Math. Res. Not. IMRN. 2010 (2010), 373–394.CrossRefGoogle Scholar
Ônishi, Y., On Weierstrass’ paper “Zur Theorie der elliptischen functionen. Available at: http://www2.meijo-u.ac.jp/~yonishi/#publications.Google Scholar
Ônishi, Y., Universal elliptic functions, 2010, http://arxiv.org/abs/1003.2927.Google Scholar
Ônishi, Y., Arithmetical power series expansion of the sigma function for a plane curve, Proc. Edinburgh Math. Soc 61(4) (2018), 995–1022.CrossRefGoogle Scholar
Ônishi, Y., Shibata, M. and Sato, K., Theory of heat equations for sigma functions II, 2024). unpublished, in preparationGoogle Scholar
Rademacher, H., Topics in analytic number theory, Die Grundlehren der mathematischen Wissenschaften, vol. 169 (Springer-Verlag, Berlin, Heidelberg, New York, 1973).CrossRefGoogle Scholar
Thomae, C. J., Beitrag zur Bestimmung von $\Theta (0,0,\ldots 0)$ durch die Klassenmoduln algebraischer Funktionen, J. für Die Reine Und Angew. Math. 7 (1870), 201–222.Google Scholar
Weierstrass, K., Zur Theorie der elliptischen functionen, Königl, Akademie der Wissenschaften 27 (1882), (Werke II, pp.245-255)Google Scholar
Zakalyukin, V. M., Reconstructions of fronts and caustics depending on a parameter and versality of mappings, J. Sov. Math. 27(3) (1984), 2713–2735.CrossRefGoogle Scholar