Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-03T02:58:13.176Z Has data issue: false hasContentIssue false
  • English
  • Français

SPECTRAL CONDITIONS FOR UNIFORM P-ERGODICITIES OF MARKOV OPERATORS ON ABSTRACT STATES SPACES

Part of: Measure-theoretic ergodic theory General theory of linear operators Markov processes

Published online by Cambridge University Press:  23 September 2020

NAZIFE ERKURŞUN-ÖZCAN  and
FARRUKH MUKHAMEDOV
NAZIFE ERKURŞUN-ÖZCAN
Affiliation:
Department of Mathematics, Faculty of Science, Hacettepe University, Ankara06800, Turkey, e-mail: [email protected]
FARRUKH MUKHAMEDOV
Affiliation:
Department of Mathematical Sciences, College of Science, United Arab Emirates University, Al Ain, Abu Dhabi15551, United Arab Emirates, e-mails: [email protected]; [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In the present paper, we deal with asymptotical stability of Markov operators acting on abstract state spaces (i.e. an ordered Banach space, where the norm has an additivity property on the cone of positive elements). Basically, we are interested in the rate of convergence when a Markov operator T satisfies the uniform P-ergodicity, i.e. 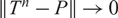$\|T^n-P\|\to 0$ , here P is a projection. 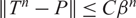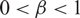We have showed that T is uniformly P-ergodic if and only if $\|T^n-P\|\leq C\beta^n$ , $0<\beta<1$ . In this paper, we prove that such a β is characterized by the spectral radius of T − P. Moreover, we give Deoblin’s kind of conditions for the uniform P-ergodicity of Markov operators.

MSC classification

Primary: 47A35: Ergodic theory
Secondary: 60J10: Markov chains (discrete-time Markov processes on discrete state spaces) 28D05: Measure-preserving transformations
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 63 , Issue 3 , September 2021 , pp. 682 - 696
Copyright
© The Author(s), 2020. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alekhno, E. A., Some properties of essential spectra of a positive operator, Positivity 11 (2007), 375–386.CrossRefGoogle Scholar
Alfsen, E. M., Compact convex sets and boundary integrals (Springer-Verlag, Berlin, 1971).CrossRefGoogle Scholar
Bartoszek, W., Asymptotic properties of iterates of stochastic operators on (AL) Banach lattices, Anal. Polon. Math. 52 (1990), 165–173.CrossRefGoogle Scholar
Bartoszek, W. and Kuna, B., On residualities in the set of Markov operators on C 1, Proc. Amer. Math. Soc. 133 (2005), 2119–2129.CrossRefGoogle Scholar
Conde-Alonso, J. M., Parcet, J. and Ricard, E., On spectral gaps of Markov maps, Israel J. Math. 226 (2018), 189–203.CrossRefGoogle Scholar
Dobrushin, R. L., Central limit theorem for nonstationary Markov chains. I,II, Theor. Probab. Appl. 1 (1956), 65–80; 329–383.CrossRefGoogle Scholar
Dorea, C. C. Y. and Pereira, A. G.C., A note on a variation of Doeblin’s condition for uniform ergodicity of Markov chains, Acta Math. Hungar. 10 (2006), 287–292.CrossRefGoogle Scholar
Dunford, N. and Schwartz, J. T., Linear operators, I. General theory (Interscience Publishers, Geneva, 1964).Google Scholar
Yu, E.. Emel’yanov, Non-spectral asymptotic analysis of one-parameter operator semigroups (Birkhäuser Verlag, Basel, 2007).Google Scholar
Yu, E.. Emel’yanov and M. P. H. Wolff, Positive operators on Banach spaces ordered by strongly normal cones, Positivity 7 (2003), 3–22.Google Scholar
Erkurşun-Özcan, N. and Mukhamedov, F., Uniform ergodicities and perturbation bounds of Markov chains on ordered Banach spaces, J. Phys. Conf. Ser. 819 (2017), 012015.CrossRefGoogle Scholar
Erkurşun-Özcan, N. and Mukhamedov, F., Uniform ergodicities and perturbation bounds of Markov chains on ordered Banach spaces, Queast. Math. 41(6) (2018), 863–876.CrossRefGoogle Scholar
Glück, J., On the peripheral spectrum of positive operators, Positivity 20(2016), 307–336.CrossRefGoogle Scholar
Hartfiel, D. J., Coefficients of ergodicity for imprimitive marices, Commun. Statis. Stochastic Models 15 (1999), 81–88.CrossRefGoogle Scholar
Hartfiel, D. J. and Rothblum, U. G., Convergence of inhomogeneous products of matrices and coefficients of ergodicity, Lin. Alg. Appl. 277 (1998), 1–9.CrossRefGoogle Scholar
Isaacson, D. and Luecke, G. R., Strongly ergodic Markov chains and rates of convergence using spectral conditions, Stochast. Process Appl. 7 (1978), 113–121.CrossRefGoogle Scholar
Jameson, G., Ordered linear spaces, Lecture Notes in Mathematics, vol. 141 (Springer-Verlag, Berlin, 1970).CrossRefGoogle Scholar
Kontoyiannis, I. and Meyn, S. P., Geometric ergodicity and the spectral gap of non-reversible Markov chains, Probab. Theory Relat. Fields 154 (2012), 327–339.CrossRefGoogle Scholar
Krengel, U., Ergodic theorems (Walter de Gruyter, Berlin-New York, 1985).CrossRefGoogle Scholar
Meyn, S. P. and Tweedie, R. L.) Markov chains and stochastic stability (Springer-Verlag, Berlin, 1996).Google Scholar
Mitrophanov, A., Sensitivity and convergence of uniform ergodic Markov chains, J. Appl. Probab. 42 (2005), 1003–1014.CrossRefGoogle Scholar
Mitrophanov, A., Stability estimates for finite homogeneous continuous-time Markov chains, Theory Probab. Appl. 50(2) (2006), 319–326.CrossRefGoogle Scholar
Mukhamedov, F., On tensor products of weak mixing vector sequences and their applications to C*-dynamical systems, Bull. Aust. Math. Soc. 85(2012), 46–59.CrossRefGoogle Scholar
Mukhamedov, F., Dobrushin ergodicity coefficient and ergodicity of noncommutative Markov chains, J. Math. Anal. Appl. 408 (2013), 364–373.CrossRefGoogle Scholar
Mukhamedov, F., Ergodic properties of nonhomogeneous Markov chains defined on ordered Banach spaces with a base, Acta. Math. Hungar. 147 (2015), 294–323.CrossRefGoogle Scholar
Mukhamedov, F., Strong and weak ergodicity of nonhomogeneous Markov chains defined on ordered Banach spaces with a base, Positivity 20 (2016), 135–153.CrossRefGoogle Scholar
Mukhamedov, F. and Al-Rawashdeh, A., On generalized Dobrushin ergodicity coefficient and uniform Ergodicites of Markov Operators, Positivity 24(4) (2020), 855–890.CrossRefGoogle Scholar
Munoz, G. A., Sarantopoulos, Y. and Tonge, A., Complexification of real Banach spaces, polynomials and miultilinear maps, Studia Math. 134 (1999), 1–33.CrossRefGoogle Scholar
Nummelin, E., General irreducible Markov chains and non-negative operators (Cambridge University Press, Cambridge 1984).CrossRefGoogle Scholar
Paz, A., Ergodic theorems for infinite probabilistic tables, Ann. Math. Statist. 41 (1970), 539–550.CrossRefGoogle Scholar
Rabiger, F., Stability and ergodicity of dominated semigroups, I. The uniform case, Math. Z. 214 (1993), 43–53.CrossRefGoogle Scholar
Reeb, D., Kastoryano, M. J. and Wolf, M. M., Hilbert’s projective metric in quantum information theory, J. Math. Phys. 52 (2011), 082201.CrossRefGoogle Scholar
Rickart, C. E., General theory of Banach algebras (Krieger, Huntington, NY 1960).Google Scholar
Sarymsakov, T. A. and Ya, G.. Grabarnik, Regularity of monotonically continuous contractions acting on the von Neumann algebra, Dokl. Akad. Nauk UzSSR 5 (1987), 9–11.Google Scholar
Sarymsakov, T. A. and Zimakov, N. P., Ergodic principle for Markov semi-groups in ordered normal spaces with basis, Dokl. Akad. Nauk. SSSR 289 (1986), 554–558.Google Scholar
Schaefer, H. H., Banach lattices and positive operators (Springer-Verlag, New York-Heidelberg, 1974).CrossRefGoogle Scholar
Szarek, T., The uniqueness of invariant measures for Markov operators, Studia Math. 189 (2008), 225–233.CrossRefGoogle Scholar
Winnkler, G., Image analysis, random fields and Markov chain Monte Carlo Methods. A mathematical introduction (Springer-Verlag, Berlin-New York-Heidelberg, 2003).Google Scholar
Wong, Y. C. and Ng, K. F., Partially ordered topological vector spaces (Clarendon Press, Oxford, 1973).Google Scholar
Yost, D., A base norm space whose cone is not 1- generating, Glasgow Math. J. 25 (1984), 35–36.CrossRefGoogle Scholar