Published online by Cambridge University Press: 11 May 2021
Let K be a field of arbitrary characteristic, 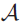 $${\cal A}$$
be a commutative K-algebra which is a domain of essentially finite type (e.g., the algebra of functions on an irreducible affine algebraic variety),
$${\cal A}$$
be a commutative K-algebra which is a domain of essentially finite type (e.g., the algebra of functions on an irreducible affine algebraic variety), 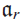 $${a_r}$$
be its Jacobian ideal, and
$${a_r}$$
be its Jacobian ideal, and 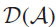 $${\cal D}\left( {\cal A} \right)$$
be the algebra of differential operators on the algebra
$${\cal D}\left( {\cal A} \right)$$
be the algebra of differential operators on the algebra 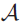 $${\cal A}$$
. The aim of the paper is to give a simplicity criterion for the algebra
$${\cal A}$$
. The aim of the paper is to give a simplicity criterion for the algebra 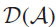 $${\cal D}\left( {\cal A} \right)$$
: the algebra
$${\cal D}\left( {\cal A} \right)$$
: the algebra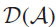 $${\cal D}\left( {\cal A} \right)$$
is simple iff
$${\cal D}\left( {\cal A} \right)$$
is simple iff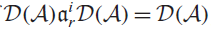 $${\cal D}\left( {\cal A} \right)a_r^i{\cal D}\left( {\cal A} \right) = {\cal D}\left( {\cal A} \right)$$
for all i ≥ 1 provided the field K is a perfect field. Furthermore, a simplicity criterion is given for the algebra
$${\cal D}\left( {\cal A} \right)a_r^i{\cal D}\left( {\cal A} \right) = {\cal D}\left( {\cal A} \right)$$
for all i ≥ 1 provided the field K is a perfect field. Furthermore, a simplicity criterion is given for the algebra 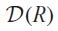 $${\cal D}\left( R \right)$$
of differential operators on an arbitrary commutative algebra R over an arbitrary field. This gives an answer to an old question to find a simplicity criterion for algebras of differential operators.
$${\cal D}\left( R \right)$$
of differential operators on an arbitrary commutative algebra R over an arbitrary field. This gives an answer to an old question to find a simplicity criterion for algebras of differential operators.