Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-26T04:04:12.061Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE σ-NILPOTENT NORM AND THE σ-NILPOTENT LENGTH OF A FINITE GROUP

Part of: Representation theory of groups

Published online by Cambridge University Press:  27 February 2020

BIN HU ,
JIANHONG HUANG Open the ORCID record for JIANHONG HUANG [Opens in a new window]  and
ALEXANDER N. SKIBA
BIN HU
Affiliation:
School of Mathematics and Statistics, Jiangsu Normal University, Xuzhou, 221116, P.R. China e-mails: [email protected]; [email protected]
JIANHONG HUANG
Affiliation:
School of Mathematics and Statistics, Jiangsu Normal University, Xuzhou, 221116, P.R. China e-mails: [email protected]; [email protected]
ALEXANDER N. SKIBA
Affiliation:
Department of Mathematics and Technologies of Programming, Francisk Skorina Gomel State University, Gomel246019, Belarus e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let G be a finite group and σ = {σi| i ∈ I} some partition of the set of all primes 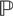$\Bbb{P}$ . Then G is said to be: σ-primary if G is a σi-group for some i; σ-nilpotent if G = G1× … × Gt for some σ-primary groups G1, … , Gt; σ-soluble if every chief factor of G is σ-primary. We use 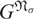$G^{{\mathfrak{N}}_{\sigma}}$ to denote the σ-nilpotent residual of G, that is, the intersection of all normal subgroups N of G with σ-nilpotent quotient G/N. If G is σ-soluble, then the σ-nilpotent length (denoted by lσ (G)) of G is the length of the shortest normal chain of G with σ-nilpotent factors. Let Nσ (G) be the intersection of the normalizers of the σ-nilpotent residuals of all subgroups of G, that is,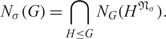

$${N_\sigma }(G) = \bigcap\limits_{H \le G} {{N_G}} ({H^{{_\sigma }}}).$$

Then the subgroup Nσ (G) is called the σ-nilpotent norm of G. We study the relationship of the σ-nilpotent length with the σ-nilpotent norm of G. In particular, we prove that the σ-nilpotent length of a σ-soluble group G is at most r (r > 1) if and only if lσ (G/ Nσ (G)) ≤ r.

MSC classification

Primary: 20D10: Solvable groups, theory of formations, Schunck classes, Fitting classes, $pi$-length, ranks
Secondary: 20D15: Nilpotent groups, $p$-groups 20D30: Series and lattices of subgroups
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 63 , Issue 1 , January 2021 , pp. 121 - 132
Copyright
© The Author(s) 2020. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Robinson, D. J. S., A Course in the theory of groups (Springer-Verlag, New York, Heidelberg, Berlin, 1982).Google Scholar
Skiba, A. N., On σ-subnormal and σ-permutable subgroups of finite groups, J. Algebra, 436 (2015), 1–16.CrossRefGoogle Scholar
Guo, W. and Skiba, A. N., Finite groups whose n-maximal subgroups are σ-subnormal, Sci. China Math. 62(7) (2019), 1355–1372.Google Scholar
Skiba, A. N., Some characterizations of finite σ-soluble PσT-groups, J. Alg. 495(1) (2018), 114–129.CrossRefGoogle Scholar
Doerk, K. and Hawkes, T., Finite soluble groups (Walter de Gruyter, Berlin, New York, 1992).CrossRefGoogle Scholar
Chunikhin, S. A., Subgroups of finite groups (Nauka i Tehnika, Minsk, 1964).Google Scholar
Guo, W. and Skiba, A. N., On σ-supersoluble groups and one generalization of CLT-groups, J. Alg. 512(1) (2018), 92–108.CrossRefGoogle Scholar
Baer, R., Kern, Der, eine charkteristishe Untergruppe, Compos. Math. 1 (1935), 254–283.Google Scholar
Baer, R., Norm and hypernorm, Publ. Math. Debrecen, 4 (1956), 347–350.Google Scholar
Shen, Z., Shi, W. and Qian, G., On the norm of the nilpotent residuals of all subgroups of a finite group, J. Alg. 352 (2012), 290–298.CrossRefGoogle Scholar
Selkin, V. M., On the π-decomposable norm of a finite group, Proceedings of Francisk Skorina Gomel State University 103(4) (2018), 51–55.Google Scholar
Selkin, V. M. and Kosenok, N. S., On the generalized norm of a finite group, Problems Phys. Math. Tech. 34(4) (2018), 69–74.Google Scholar
Ballester-Bolinches, A. and Ezquerro, L. M., Classes of finite groups (Springer, Dordrecht, 2006).Google Scholar
Hu, B., Huang, J. and Skiba, A. N., Characterizations of finite σ-nilpotent and σ-quasinilpotent groups, Bull. Malays. Math. Soc. 42(5) (2019), 2091–2104.Google Scholar
Su, N. and Wang, Y., On the normalizers of $\mathfrak{F}$ -residuals of all subgroups of a finite group, J. Alg. 392 (2013), 185–198.CrossRefGoogle Scholar
Belonogov, V. A., Finite groups all of whose 2-maximal subgroups are π-decomposable, Trudi Instituta Matematiki i Mekhaniki Uro RAN 20(2) (2014), 29–43.Google Scholar
Huppert, B., Endliche Gruppen I (Springer-Verlag, Berlin, Heidelberg, New York, 1967).CrossRefGoogle Scholar
Gorenstein, D., Finite groups (Harper & Row Publishers, New York, Evanston, London, 1968).Google Scholar
Shemetkov, L.A., Formations of finite groups (Nauka, Moscow, 1978).Google Scholar