Hostname: page-component-669899f699-swprf Total loading time: 0 Render date: 2025-04-24T12:55:58.118Z Has data issue: false hasContentIssue false
  • English
  • Français

On a weighted anisotropic eigenvalue problem

Part of: Elliptic equations and systems Partial differential equations

Published online by Cambridge University Press:  17 October 2024

Nunzia Gavitone  and
Rossano Sannipoli
Nunzia Gavitone*
Affiliation:
Dipartimento di Matematica e Applicazioni “R. Caccioppoli”. Università degli Studi di Napoli Federico II, 80126, Napoli, Italy
Rossano Sannipoli
Affiliation:
Dipartimento di Matematica “Tullio Levi-Civita”, Universitá degli Studi di Padova, 35131, Padova, Italy
*
Corresponding author: Nunzia Gavitone; Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we deal with a weighted eigenvalue problem for the anisotropic 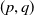$(p,q)$-Laplacian with Dirichlet boundary conditions. We study the main properties of the first eigenvalue and a reverse Hölder type inequality for the corresponding eigenfunctions.

Keywords

Anisotropic p-LaplacianComparison resultsReverse Hölder inequality

MSC classification

Primary: 35B51: Comparison principles 35J62: Quasilinear elliptic equations
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 67 , Issue 1 , January 2025 , pp. 72 - 85
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Alberico, A., Ferone, A. and Volpicelli, R., Some properties for eigenvalues and eigenfunctions of nonlinear weighted problems, Rend. Mat. Appl 19(1) (1999), 45–63.Google Scholar
Alvino, A., Ferone, V., Lions, P.-L. and Trombetti, G., Convex symmetrization and applications, Ann. Inst. H. Poincaré C Anal. Non Linéaire 14(2) (1997), 275–293.Google Scholar
Alvino, A., Ferone, V. and Trombetti, G., On the properties of some nonlinear eigenvalues, SIAM J. Math. Anal. 29(2) (1998), 437–451.CrossRefGoogle Scholar
Alvino, A., Lions, P.-L. and Trombetti, G., On optimization problems with prescribed rearrangements, Nonlinear Anal. Theory Methods Appl. 13(2) (1989), 185–220.CrossRefGoogle Scholar
Alvino, A., Trombetti, G. and Lions, P.-L., Comparison results for elliptic and parabolic equations via Schwarz symmetrization, Ann. Inst. H. Poincaré C Anal. Non Linéaire 7(2) (1990), 37–65.Google Scholar
Amar, M. and Bellettini, G., A notion of total variation depending on a metric with discontinuous coefficients, Ann. Inst. H. Poincaré C Anal. Non Linéaire 11(1) (1994), 91–133.CrossRefGoogle Scholar
Amato, V., Barbato, R., Masiello, A. L. and Paoli, G., The Talenti comparison result in a quantitative form (2023). arXiv preprint.CrossRefGoogle Scholar
Bellettini, G., Caselles, V., Chambolle, A. and Novaga, M., The volume preserving crystalline mean curvature flow of convex sets in $\Bbb R^N$ , J. Math. Pures Appl. (9) 92(5) (2009), 499–527.CrossRefGoogle Scholar
Belloni, M., Ferone, V. and Kawohl, B., Isoperimetric inequalities, Wulff shape and related questions for strongly nonlinear elliptic operators, Zeitschrift fur Angewandte Mathematik und Physik (ZAMP) 54(5) (2003), 771–783.CrossRefGoogle Scholar
Brasco, L. and Franzina, G., Convexity properties of Dirichlet integrals and Picone-type inequalities, Kodai Math. J. 37(3) (2014), 769–799.CrossRefGoogle Scholar
Brasco, L. and Franzina, G., An overview on constrained critical points of Dirichlet integrals, Rend. Semin. Mat. Univ. Politec. Torino 78(2) (2020), 7–50.Google Scholar
Busemann, H., The isoperimetric problem for Minkowski area, Am. J. Math. 71(4) (1949), 743–762.CrossRefGoogle Scholar
Carroll, T., Fall, M. M. and Ratzkin, J., On the rate of change of the sharp constant in the Sobolev-Poincaré inequality, Math. Nachr. 290(14-15) (2017), 2185–2197.CrossRefGoogle Scholar
Carroll, T. and Ratzkin, J., A reverse Hölder inequality for extremal sobolev functions, Potential Anal. 42(1) (2015), 283–292.CrossRefGoogle Scholar
Chiti, G., An isoperimetric inequality for the eigenfunctions of linear second order elliptic operators, Boll. Un. Mat. Ital. 1(1) (1982), 145–151.Google Scholar
Chiti, G., A reverse Hölder inequality for the eigenfunctions of linear second order elliptic operators, Zeitschrift für Angewandte Mathematik und Physik ZAMP 33(1) (1982), 143–148.CrossRefGoogle Scholar
Chong, K. M. and Rice, N. M., Equimeasurable rearrangements of functions, Queen’s Paper Pure Appl. Math. 28 (1971).Queen’s University, Ontario.Google Scholar
Dacorogna, B. and Pfister, C.-E., Wulff theorem and best constant in Sobolev inequality, J. Math. Pures et Appl. 71(2) (1992), 97–118.Google Scholar
Della Pietra, F. and Gavitone, N., Sharp bounds for the first eigenvalue and the torsional rigidity related to some anisotropic operators, Math. Nachr. 287(2-3) (2013), 194–209.CrossRefGoogle Scholar
Drábek, P., Kufner, A. and Nicolosi, F., Quasilinear elliptic equations with degenerations and singularities, De Gruyter Series in Nonlinear Analysis and Applications, vol. 5 (Walter de Gruyter & Co, Berlin, 1997).CrossRefGoogle Scholar
Evans, L. C. and Gariepy, R. F., Measure theory and fine properties of functions, in Textbooks in mathematics (CRC Press, Boca Raton, FL, 2015).Google Scholar
Ferone, A. and Volpicelli, R., Convex rearrangement: equality cases in the Pólya-Szegö inequality, Calc. Var. Partial Differ. Equations 21(3) (2004), 259–272.Google Scholar
Figalli, A., Maggi, F. and Pratelli, A., A mass transportation approach to quantitative isoperimetric inequalities, Invent. Math. 182(1) (2010), 167–211.CrossRefGoogle Scholar
Fonseca, I. and Müller, S., A uniqueness proof for the Wulff theorem, Proc. R. Soc. Edinburgh Sect. A Math. 119(1-2) (1991), 125–136.CrossRefGoogle Scholar
Franzina, G. and Lamberti, P. D., Existence and uniqueness for a p-Laplacian nonlinear eigenvalue problem, Electron. J. Differ. Equations 26 (2010), 1–10.Google Scholar
García Azorero, J. P. and Peral Alonso, I., Existence and nonuniqueness for the p-Laplacian: nonlinear eigenvalues, Commun. Partial Differ. Equations 12(12) (1987), 1389–1430.CrossRefGoogle Scholar
Idogawa, T. and Ôtani, M., The first eigenvalues of some abstract elliptic operators, Funkcialaj Ekvacioj 38(1) (1995), 1–9.Google Scholar
Kawohl, B., Symmetry results for functions yielding best constants in Sobolev-type inequalities, Discrete Contin. Dyn. Syst. 6(3) (2000), 683–690.CrossRefGoogle Scholar
Kawohl, B., Lucia, M. and Prashanth, S., Simplicity of the principal eigenvalue for indefinite quasilinear problems, Adv. Differ. Equations 12(4) (2007), 407–434.CrossRefGoogle Scholar
Kesavan, S., Symmetrization and applications, in: Series in Analysis, vol. 3 (World Scientific Publishing Co. Pte. Ltd., New Jersey, 2006).CrossRefGoogle Scholar
Maggi, F., Sets of finite perimeter and geometric variational problems, in Cambridge studies in advanced mathematics, vol. 135 (Cambridge University Press, Cambridge, 2012).Google Scholar
Nazarov, A. I., The one-dimensional character of an extremum point of the Friedrichs inequality in spherical and plane layers, J. Math. Sci. 102(5) (2000), 4473–4486.CrossRefGoogle Scholar
Nazarov, A. I., On the symmetry of extremals in the weight embedding theorem, J. Math. Sci. (New York) 107(3) (2001), 3841–3859.CrossRefGoogle Scholar
Ôtani, M., On certain second order ordinary differential equations associated with Sobolev-Poincaré-type inequalities, Nonlinear Anal. Theory Methods Appl. 8(11) (1984), 1255–1270.CrossRefGoogle Scholar
Ôtani, M., Existence and nonexistence of nontrivial solutions of some nonlinear degenerate elliptic equations, J. Funct. Anal. 76(1) (1988), 140–159.CrossRefGoogle Scholar
Sannipoli, R., Comparison results for solutions to the anisotropic Laplacian with Robin boundary conditions, Nonlinear Anal. 214 (2022), 112615.CrossRefGoogle Scholar
Talenti, G., Elliptic equations and rearrangements, Ann. Scuola Norm-SCI 3(4) (1976), 697–718.Google Scholar
Ziemer, W. P. and Brothers, J. E., Minimal rearrangements of Sobolev functions, Journal für die reine und angewandte Mathematik 384 (1988), 153–179.CrossRefGoogle Scholar