No CrossRef data available.
Published online by Cambridge University Press: 21 March 2019
For a path connected space X, the homology algebra 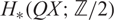 $H_*(QX; \mathbb{Z}/2)$ is a polynomial algebra over certain generators QIx. We reinterpret a technical observation, of Curtis and Wellington, on the action of the Steenrod algebra A on the Λ algebra in our terms. We then introduce a partial order on each grading of H*QX which allows us to separate terms in a useful way when computing the action of dual Steenrod operations
$H_*(QX; \mathbb{Z}/2)$ is a polynomial algebra over certain generators QIx. We reinterpret a technical observation, of Curtis and Wellington, on the action of the Steenrod algebra A on the Λ algebra in our terms. We then introduce a partial order on each grading of H*QX which allows us to separate terms in a useful way when computing the action of dual Steenrod operations 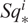 $Sq^i_*$ on
$Sq^i_*$ on 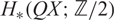 $H_*(QX; \mathbb{Z}/2)$. We use these to completely characterise the A-annihilated generators of this polynomial algebra. We then propose a construction for sequences I so that QIx is A-annihilated. As an application, we offer some results on the form of potential spherical classes in H*QX upon some stability condition under homology suspension. Our computations provide new numerical conditions in the context of hit problem.
$H_*(QX; \mathbb{Z}/2)$. We use these to completely characterise the A-annihilated generators of this polynomial algebra. We then propose a construction for sequences I so that QIx is A-annihilated. As an application, we offer some results on the form of potential spherical classes in H*QX upon some stability condition under homology suspension. Our computations provide new numerical conditions in the context of hit problem.