Hostname: page-component-6bf8c574d5-b4m5d Total loading time: 0 Render date: 2025-02-28T17:00:50.642Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-additive derived functors via chain resolutions

Part of: Homological algebra

Published online by Cambridge University Press:  28 February 2025

Maxime Culot ,
Fara Renaud  and
Tim Van der Linden Open the ORCID record for Tim Van der Linden [Opens in a new window]
Maxime Culot
Affiliation:
Institut de Recherche en Mathématique et Physique, Université catholique de Louvain, 1348 Louvain-la-Neuve, Belgium
Fara Renaud
Affiliation:
Institut de Recherche en Mathématique et Physique, Université catholique de Louvain, 1348 Louvain-la-Neuve, Belgium
Tim Van der Linden*
Affiliation:
Institut de Recherche en Mathématique et Physique, Université catholique de Louvain, 1348 Louvain-la-Neuve, Belgium Mathematics & Data Science, Vrije Universiteit Brussel, 1050 Brussel, Belgium
*
Corresponding author: Tim Van der Linden; Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 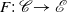$F:\; {\mathscr {C}} \to {\mathscr {E}} \ $ be a functor from a category $\mathscr {C} \ $ to a homological (Borceux–Bourn) or semi-abelian (Janelidze–Márki–Tholen) category 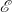$\mathscr {E}$. We investigate conditions under which the homology of an object 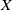$X$ in 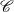$\mathscr {C}$ with coefficients in the functor 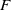$F$, defined via projective resolutions in 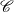$\mathscr {C}$, remains independent of the chosen resolution. Consequently, the left derived functors of 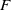$F$ can be constructed analogously to the classical abelian case.

Our approach extends the concept of chain homotopy to a non-additive setting using the technique of imaginary morphisms. Specifically, we utilize the approximate subtractions of Bourn–Janelidze, originally introduced in the context of subtractive categories. This method is applicable when $\mathscr {C}$ is a pointed regular category with finite coproducts and enough projectives, provided the class of projectives is closed under protosplit subobjects, a new condition introduced in this article and naturally satisfied in the abelian context. We further assume that the functor 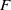$F$ meets certain exactness conditions: for instance, it may be protoadditive and preserve proper morphisms and binary coproducts—conditions that amount to additivity when 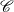$\mathscr {C}$ and $\mathscr {E}$ are abelian categories.

Within this framework, we develop a basic theory of derived functors, compare it with the simplicial approach, and provide several examples.

Keywords

Derived functornormal subtractive categoryhomological categorysemi-abelian categorychain homotopysimplicial homotopyapproximate subtractionprotosplit subobjectprojective object

MSC classification

Primary: 18G05: Projectives and injectives 18G10: Resolutions; derived functors
Type
Research Article
Information
Glasgow Mathematical Journal , First View , pp. 1 - 44
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bahturin, Yu. A., Identical relations in Lie algebras. (VNU Science Press, Utrecht, 1987).Google Scholar
Barr, M. and Beck, J., Homology and standard constructions, Seminar on triples and categorical homology theory (ETH, Zürich, 1966/67), Lecture Notes in Math., vol. 80 (Springer, 1966/67)), 245–335, 1969.CrossRefGoogle Scholar
Barr, M., Grillet, P. A. and van Osdol, D. H., Exact categories and categories of sheaves, Lecture notes in math, vol. 236 (Springer, 1971).Google Scholar
Borceux, F., Handbook of categorical algebra 1: basic category theory, Encyclopedia Math. Appl, vol. 50 (Cambridge Univ. Press, 1994).Google Scholar
Borceux, F. and Bourn, D., Mal’cev, protomodular, homological and semi-abelian categories, Math. Appl, vol. 566 (Kluwer Acad. Publ., 2004).Google Scholar
Borceux, F., Janelidze, G. and Kelly, G. M., Internal object actions, Comment. Math. Univ. Carolinae 46 (2005), 235–255.Google Scholar
Bourbaki, N., Lie groups and Lie algebras, part I (Chapters 1-3). (Elements of Mathematics, Addison-Wesley, 1975).Google Scholar
Bourn, D., Normalization equivalence, kernel equivalence and affine categories, Category Theory, Proceedings Como 1990, (Carboni, A., Pedicchio, M. C. and Rosolini, G. eds.) Lecture Notes in Math, vol. 1488 (Springer, 1991), 43–62.Google Scholar
Bourn, D., $3\times 3$ lemma and protomodularity, J. Algebra 236 (2001), 778–795.CrossRefGoogle Scholar
Bourn, D., Intrinsic centrality and associated classifying properties, J. Algebra 256(1) (2002), 126–145.CrossRefGoogle Scholar
Bourn, D., The denormalized $3\times 3$ lemma, J. Pure Appl. Algebra 177 (2003), 113–129.CrossRefGoogle Scholar
Bourn, D., Moore normalization and Dold-Kan theorem for semi-abelian categories, Contemp. Math. 431 (2006), 105–124.CrossRefGoogle Scholar
Bourn, D. and Janelidze, G., Protomodularity, descent, and semidirect products, Theory Appl. Categ. 4(2) (1998), 37–46.Google Scholar
Bourn, D. and Janelidze, G., Characterization of protomodular varieties of universal algebras, Theory Appl. Categ. 11 (6) (2003), 143–147.Google Scholar
Bourn, D. and Janelidze, Z., Pointed protomodularity via natural imaginary subtractions, J. Pure Appl. Algebra 213(9) (2009), 1835–1851.CrossRefGoogle Scholar
Bourn, D. and Janelidze, Z., Subtractive categories and extended subtractions, Appl. Categ. Structures 17(4) (2009), 317–343.CrossRefGoogle Scholar
Brown, K. S., Abstract homotopy theory and generalized sheaf cohomology. Trans. Amer. Math. Soc. 186 (1973), 419–458.CrossRefGoogle Scholar
Brown, R. and Spencer, C. B., G-groupoids, crossed modules and the fundamental groupoid of a topological group, Indag. Math. (Proc.) 79 (4) (1976), 296–302.CrossRefGoogle Scholar
Carboni, A., Kelly, G. M. and Pedicchio, M. C., Some remarks on Maltsev and Goursat categories, Appl. Categ. Structures 1(4) (1993), 385–421.CrossRefGoogle Scholar
Carrasco, P. and Cegarra, A. M., Group-theoretic algebraic models for homotopy types, J. Pure Appl. Algebra 75(3) (1991), 195–235.CrossRefGoogle Scholar
Carrasco, P., Cegarra, A. M. and Grandjeán, A. R.-, (Co)Homology of crossed modules, J. Pure Appl. Algebra 168(2-3) (2002), 147–176.CrossRefGoogle Scholar
Cartan, H., Eilenberg, S. and Homological algebra, (Princeton University Press, 1956).CrossRefGoogle Scholar
Clementino, M. M., Gran, M. and Janelidze, G., Some remarks on protolocalizations and protoadditive reflections, J. Algebra Appl. 17(11) (2018), 1850207.CrossRefGoogle Scholar
Clementino, M. M., Martins-Ferreira, N. and Montoli, A., On the categorical behaviour of preordered groups, J. Pure Appl. Algebra 223 (10) (2019), 4226–4245.CrossRefGoogle Scholar
Culot, M. and Van der Linden, T., Projective crossed modules in semi-abelian categories, in preparation, (2024).Google Scholar
Dold, A., Homology of symmetric products and other functors of complexes, Ann. of Math. 68(1) (1958), 54–80.CrossRefGoogle Scholar
Dold, A. and Puppe, D., Homologie nicht-additiver Funktoren. Anwendungen, Ann. Inst. Fourier (Grenoble) 11 (1961), 201–312.CrossRefGoogle Scholar
Donadze, G. and Van der Linden, T., A comonadic interpretation of Baues-Ellis homology of crossed modules, J. Homotopy Relat. Struct. 14(3) (2019), 625–646.CrossRefGoogle Scholar
Dotsenko, V. and Umirbaev, U., An effective criterion for Nielsen-Schreier varieties, Math. Res. Not. IMRN (2023), no. 23, 20385–20432.CrossRefGoogle Scholar
Everaert, T., Goedecke, J. and Van der Linden, T., Resolutions, higher extensions and the relative Mal’tsev axiom, J. Algebra 371 (2012), 132–155.CrossRefGoogle Scholar
Everaert, T. and Gran, M., Homology of $n$ -fold groupoids, Theory Appl. Categ. 23 (2) (2010), 22–41.Google Scholar
Everaert, T. and Gran, M., Protoadditive functors, derived torsion theories and homology, J. Pure Appl. Algebra 219(8) (2015), 3629–3676.CrossRefGoogle Scholar
Everaert, T., Gran, M. and Van der Linden, T., Higher Hopf formulae for homology via Galois theory, Adv. Math. 217(5) (2008), 2231–2267.CrossRefGoogle Scholar
Everaert, T. and Van der Linden, T., Baer invariants in semi-abelian categories II: Homology, Theory Appl. Categ. 12(4) (2004), 195–224.Google Scholar
Freyd, P., Abelian categories, Harper and Row, republished in, Reprints in Theory and Applications of Categories 2003(3) (1964), New York.Google Scholar
Goedecke, J., Three viewpoints on semi-abelian homology, Ph.D. thesis. University of Cambridge; 2009.Google Scholar
Goedecke, J., Homology in relative semi-abelian categories, Appl. Categ. Structures 21(6) (2013), 523–543.CrossRefGoogle Scholar
Goedecke, J. and Van der Linden, T., A comparison theorem for simplicial resolutions, J. Homotopy Relat. Struct. 2(1) (2007), 109–126.Google Scholar
Grandis, M., Homological algebra, in strongly non-abelian settings. (World Scientific Publishing, Singapore, 2013).CrossRefGoogle Scholar
Higgins, P. J., Groups with multiple operators, Proc. Lond. Math. Soc. 6 (3) (1956), 366–416.CrossRefGoogle Scholar
Hilton, P. J. and Stammbach, U., A course in homological algebra, second ed. Graduate Texts in Mathematics, vol. 4, (Springer, 1971).CrossRefGoogle Scholar
Inasaridze, H. N., Homotopy of pseudosimplicial groups, nonabelian derived functors, and algebraic $K$ -theory, Mat. Sb. (N.S.) 98(140) (1975), no. 3(11), 339–362, 495.Google Scholar
Inassaridze, H., Non-abelian homological algebra and its applications, Mathematics and its applications, vol. 421 (Kluwer Academic Publishers, Dordrecht, 1997).Google Scholar
Janelidze, G., Internal crossed modules, Georgian Math. J. 10(1) (2003), 99–114.CrossRefGoogle Scholar
Janelidze, G., Galois groups, abstract commutators and Hopf formula, Appl. Categ. Structures 16(6) (2008), 653–668.CrossRefGoogle Scholar
Janelidze, G., Márki, L. and Tholen, W., Semi-abelian categories, J. Pure Appl. Algebra 168(2-3) (2002), 367–386.CrossRefGoogle Scholar
Janelidze, Z., Subtractive categories, Appl. Categ. Structures 13(4) (2005), 343–350.CrossRefGoogle Scholar
Janelidze, Z., The pointed subobject functor, $3\times 3$ lemmas, and subtractivity of spans, Theory Appl. Categ. 23(11) (2010), 221–242.Google Scholar
Johnsson, D. L., Topics in the theory of group presentations, 1 ed. London Mathematical Society Lecture Note Series, 42, (Cambridge University Press, 1980).CrossRefGoogle Scholar
Kurosh, A., Nonassociative free algebras and free products of algebras, Mat. Sb. 20(62) (1947), no. 2, 236–262, in Russian.Google Scholar
Lazard, M., Groupes, anneaux de Lie et problème de Burnside, Gruppi, anelli di Lie e teoria della coomologia, (Inst. Math. dell’Università Roma, 1959), 123–184.CrossRefGoogle Scholar
Loday, J.-L., Spaces with finitely many non-trivial homotopy groups, J. Pure Appl. Algebra 24(2) (1982), 179–202.CrossRefGoogle Scholar
MacDonald, J. L., Group derived functors, J. Algebra 10(4) (1968), 448–477.CrossRefGoogle Scholar
Lane, S. Mac, Homology, Grundlehren der mathematischen Wissenschaften, vol. 114 (Springer, 1967).Google Scholar
Lane, S. Mac, Categories for the working mathematician, second ed., Grad. Texts in Math, vol. 5 (Springer, 1998).Google Scholar
Lane, S. Mac and Whitehead, J. H. C., On the $3$ -type of a complex, Proc. Nat. Acad. Sci. U.S.A 36 (1950), 41–48.Google Scholar
Mal’cev, A. I., Algebraic systems, Grundlehren der mathematischen Wissenschaften, vol. 192 (Springer, 1973).CrossRefGoogle Scholar
Mikhalev, A. A., Subalgebras of free colored Lie superalgebras, Mat. Zametki 37 (1985), 653–661.Google Scholar
Nielsen, J., Om regning med ikke-kommutative faktorer og dens Anvendelse i Gruppeteorien, Mat. Tidsskrift B (1921), 77–94.Google Scholar
Peschke, G. and Van der Linden, T., The Yoneda isomorphism commutes with homology, J. Pure Appl. Algebra 220(2) (2016), 495–517.CrossRefGoogle Scholar
Quillen, D. G., Homotopical algebra, Lecture notes in math vol. 43 (Springer, 1967).CrossRefGoogle Scholar
Reutenauer, C., Free Lie algebras, London mathematical society monographs new series, vol. 7 (Claredon Press, 1993).CrossRefGoogle Scholar
Rodelo, D. and Van der Linden, T., The third cohomology group classifies double central extensions, Theory Appl. Categ. 23(8) (2010), 150–169.Google Scholar
Rodelo, D. and Van der Linden, T., Higher central extensions via commutators, Theory Appl. Categ. 27 (9) (2012), 189–209.Google Scholar
Rodelo, D. and Van der Linden, T., Higher central extensions and cohomology, Adv. Math. 287 (2016), 31–108.CrossRefGoogle Scholar
Schreier, O., Die Untergruppen der freien Gruppen, Abh. Math. Sem. Univ. Hamburg 5(1) (1927), 161–183.CrossRefGoogle Scholar
Shestakov, I. P. and Umirbaev, U. U., Free Akivis algebras, primitive elements, and hyperalgebras, J. Algebra 250(2) (2022), 533–548.CrossRefGoogle Scholar
Shirshov, A. I., On subalgebras of free Lie algebras, Mat. Sb. 33(75) (1953), no. 2, 441–453, in Russian.Google Scholar
Shirshov, A. I., Subalgebras of free commutative and free anticommutative algebras, Mat. Sb. 34(76) (1954), no. 1, 81–88, in Russian.Google Scholar
Shtern, A. S., Free Lie superalgebras, Sib. Math. J. 27 (1986), 136–140.CrossRefGoogle Scholar
Tierney, M. and Vogel, W., Simplicial derived functors, Category theory, Homology Theory and their Applications I, Lecture Notes in Math, vol. 86 (Springer, 1969), 167–180.CrossRefGoogle Scholar
Tierney, M. and Vogel, W., Simplicial resolutions and derived functors, Math. Z. 111(1) (1969), 1–14.CrossRefGoogle Scholar
Umirbaev, U. U., Schreier varieties of algebras, Algebra Logic 33(3) (1994), 180–193.CrossRefGoogle Scholar
Ursini, A., On subtractive varieties I, Algebr. Univ. 31(2) (1994), 204–222.CrossRefGoogle Scholar
Van der Linden, T., Homology and homotopy in semi-abelian categories, Ph.D. thesis. (Vrije Universiteit Brussel, 2006). arXiv:math/0607100v1.Google Scholar
Van der Linden, T., Simplicial homotopy in semi-abelian categories, J. K-Theory 4(2) (2009), 379–390.CrossRefGoogle Scholar
Van der Linden, T. Non-associative algebras, New perspectives in Algebra, Topology and Categories (Clementino M. M., Facchini A. and Marino G. eds.) vol. 1 (Springer, 2021), 225–258.CrossRefGoogle Scholar
Weibel, Ch. A., An introduction to homological algebra, Cambridge Studies in Advanced Mathematics, vol. 38 (Cambridge Univ. Press, 1994).Google Scholar
Whitehead, J. H. C., Combinatorial homotopy II, Bull. Amer. Math. Soc. 55(5) (1949), 453–496.CrossRefGoogle Scholar
Witt, E., Die Unterringe der freien lieschen Ringe, Math. Z., 64(1956), 195–216, in German.CrossRefGoogle Scholar