No CrossRef data available.
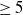 $\geq 5$
$\geq 5$Published online by Cambridge University Press: 30 January 2025
The delta invariant interprets the criterion for the K-(poly)stability of log terminal Fano varieties. In this paper, we determine local delta invariants for all weak del Pezzo surfaces with the anti-canonical degree 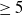 $\geq 5$.
$\geq 5$.