Hostname: page-component-745bb68f8f-f46jp Total loading time: 0 Render date: 2025-02-09T13:57:30.518Z Has data issue: false hasContentIssue false
  • English
  • Français

Hausdorff dimension of sets defined by almost convergent binary expansion sequences

Part of: Classical measure theory Probabilistic theory: distribution modulo $1$; metric theory of algorithms

Published online by Cambridge University Press:  13 March 2023

Qing-Yao Song
Qing-Yao Song*
Affiliation:
School of Mathematics and Statistics, Huazhong University of Science and Technology, Wuhan 430074, P. R. China
*
E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we study the Hausdorff dimension of sets defined by almost convergent binary expansion sequences. More precisely, the Hausdorff dimension of the following set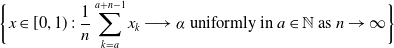

\begin{align*} \bigg\{x\in[0,1)\;:\;\frac{1}{n}\sum_{k=a}^{a+n-1}x_{k}\longrightarrow\alpha\textrm{ uniformly in }a\in\mathbb{N}\textrm{ as }n\rightarrow\infty\bigg\} \end{align*}
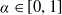is determined for any $ \alpha\in[0,1] $. This completes a question considered by Usachev [Glasg. Math. J. 64 (2022), 691–697] where only the dimension for rational $ \alpha $ is given.

Keywords

almost convergent sequenceHausdorff dimension

MSC classification

Primary: 28A80: Fractals
Secondary: 11K31: Special sequences
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 65 , Issue 2 , May 2023 , pp. 450 - 456
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Besicovitch, A., On the sum of digits of real numbers represented in the dyadic system, Math. Ann. 110 (1935), 321–330.CrossRefGoogle Scholar
Borel, É., Les probabilités dénombrables et leurs applications arithmétiques, Rend. Circ. Mat. Parlemo 26 (1909), 247–271.CrossRefGoogle Scholar
Connor, J., Almost none of the sequences of 0’s and 1’s are almost convergent, Int. J. Math. Math. Sci. 13 (1990), 775–777.CrossRefGoogle Scholar
Esi, A. and Necdet, M. çatalbaş, Almost convergence of triple sequences, Global J. Math. A 2 (2014), 6–10.Google Scholar
Falconer, K., Fractal geometry, Mathematical Foundations and Applications, 2nd edition (John Wiley & Sons, Hoboken, NJ, 2003).CrossRefGoogle Scholar
Lorentz, G., A contribution to the theory of divergent sequences, Acta Math. 80 (1948), 167–190.CrossRefGoogle Scholar
Mohiuddine, S., An application of almost convergence in approximation theorems, App. Math. L. 24 (2011), 1856–1860.CrossRefGoogle Scholar
Usachev, A., Hausdorff dimension of the set of almost convergent sequences, Glasg. Math. J. 64 (2022), 691–697.CrossRefGoogle Scholar