Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-23T14:33:41.487Z Has data issue: false hasContentIssue false
  • English
  • Français

CELLULAR AUTOMATA OVER ALGEBRAIC STRUCTURES

Part of: Topological dynamics Algebraic structures

Published online by Cambridge University Press:  26 April 2021

ALONSO CASTILLO-RAMIREZ ,
O. MATA-GUTIÉRREZ  and
ANGEL ZALDIVAR-CORICHI
ALONSO CASTILLO-RAMIREZ
Affiliation:
Department of Mathematics, University Centre of Exact Sciences and Engineering, University of Guadalajara, Guadalajara, México e-mails: [email protected], [email protected], [email protected]
O. MATA-GUTIÉRREZ
Affiliation:
Department of Mathematics, University Centre of Exact Sciences and Engineering, University of Guadalajara, Guadalajara, México e-mails: [email protected], [email protected], [email protected]
ANGEL ZALDIVAR-CORICHI
Affiliation:
Department of Mathematics, University Centre of Exact Sciences and Engineering, University of Guadalajara, Guadalajara, México e-mails: [email protected], [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let G be a group and A a set equipped with a collection of finitary operations. We study cellular automata 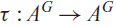$$\tau :{A^G} \to {A^G}$$ that preserve the operations AG of induced componentwise from the operations of A. We show τ that is an endomorphism of AG if and only if its local function is a homomorphism. When A is entropic (i.e. all finitary operations are homomorphisms), we establish that the set EndCA(G;A), consisting of all such endomorphic cellular automata, is isomorphic to the direct limit of Hom(AS, A), where S runs among all finite subsets of G. In particular, when A is an R-module, we show that EndCA(G;A) is isomorphic to the group algebra 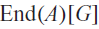$${\rm{End}}(A)[G]$$ . Moreover, when A is a finite Boolean algebra, we establish that the number of endomorphic cellular automata over AG admitting a memory set S is precisely 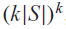$${(k|S|)^k}$$ , where k is the number of atoms of A.

MSC classification

Primary: 08A62: Finitary algebras 37B15: Cellular automata
Secondary: 06E99: None of the above, but in this section 08A35: Automorphisms, endomorphisms
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 64 , Issue 2 , May 2022 , pp. 306 - 319
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Burris, S. and Sankappanavar, H. P., A course in universal algebra (The Millennium Edition, New York, 2012).Google Scholar
Ceccherini-Silberstein, T. and Coornaert, M., The Garden of Eden theorem for linear cellular automata, Ergod. Theory Dyn. Syst. 26 (2006), 53–68.CrossRefGoogle Scholar
Ceccherini-Silberstein, T. and Coornaert, M., Injective linear cellular automata and sofic groups, Israel J. Math. 161 (2007), 1–15.CrossRefGoogle Scholar
Ceccherini-Silberstein, T. and Coornaert, M., Cellular automata and groups, Springer Monographs in Mathematics (Springer-Verlag, Berlin, Heidelberg, 2010).CrossRefGoogle Scholar
Cook, M., Universality in elementary cellular automata, Complex Syst. 15 (2004), 1–40.Google Scholar
Evans, T., Endomorphisms of abstract algebras, Proc. R. Soc. Edinb. Sect. A 66 (1962), 53–64.Google Scholar
Grätzer, G., Universal algebra, Second Edition (Springer-Verlag, New York, 2008).CrossRefGoogle Scholar
Givant, S. and Halmos, P., Introduction to boolean algebras, Undergraduate Texts in Mathematics (Springer-Verlag, New York, 2009).Google Scholar
Klukovits, L., On commutative universal algebras, Acta Sci. Math. 34 (1973), 171–174.Google Scholar
Lehtonen, E. and Pilitowska, A., Entropicity and generalized entropic property in idempotent n -semigroups, Semigroup Forum 91 (2015), 260–281.CrossRefGoogle Scholar
McLane, S., Categories for the working mathematician, Graduate Texts in Mathematics, vol. 5 (Springer-Verlag, New York, 1998).Google Scholar
Milies, C. P. and Sehgal, S. K., An introduction to group rings (Kluwer Academic Publishers, Dordrecht, 2002).CrossRefGoogle Scholar
Morris, S. A., Topology without tears, 2017. Available from author’s web site.Google Scholar
Rotman, J. J., An introduction to homological algebra, Second Edition (Springer, New York, 2009).CrossRefGoogle Scholar
Salo, V. and Törmä, I., On shift spaces with algebraic structure, In How the world computes. CiE 2012 (Cooper, S. B., Dawar, A., Lwe, B. Editors), LNCS, vol. 7318 (Springer, Berlin, Heidelberg, 2012).Google Scholar
Wolfram, S., A new kind of science (Wolfram Media, Champaign, IL, 2002).Google Scholar