Article contents
40Ar–39Ar geochronology and palaeostress analysis using lamprophyre dikes and quartz veins in the Sizhuang gold deposit: new implications for Early Cretaceous stress regime in the Jiaodong Peninsula, North China Craton
Published online by Cambridge University Press: 21 October 2022
Abstract
Lamprophyre dikes and quartz veins in the Sizhuang gold deposit are used to date and unravel the Early Cretaceous stress regime in the Jiaodong Peninsula, North China Craton. The lamprophyre dikes are grouped into two major sets, trending NNW–SSE and NNE–SSW, respectively, and a subsidiary one, trending WNW–ESE, whereas the quartz veins trend mainly NNE–SSW. The age of lamprophyre dikes’ intrusion was robustly calculated at c. 119 Ma by phlogopite 40Ar–39Ar dating. The fuzzy clustering technique defined four stress states, which were grouped into three stress regimes in Sizhuang. Furthermore, these stress regimes were interrelated with two regional far-field stress regimes, ST1 and ST2, defined by the available published fault-slip data near Sizhuang by applying the separation and stress inversion TR method (TRM). The palaeostress reconstruction indicates that extension and strike-slip tectonics (i.e. transtension) affect the emplacement of the lamprophyre dikes and quartz veins. More precisely, the dike emplacement occurred under unstable stress conditions related to the shift from E–W pure extension–transtension to WNW–ESE transtension, whereas the quartz veins formed under relatively stable WNW–ESE transtension with the variant and increasing fluid pressure (
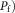 ${P_{\rm{f}}})$
giving rise to the strike-slip against dip-slip kinematics along the faults. The change from the ST1 to ST2 stress regimes reflects the significant clockwise rotation in the palaeo-Pacific plate subduction direction and defines the switching time at c. 119 Ma as precisely obtained by the lamprophyre dating.
${P_{\rm{f}}})$
giving rise to the strike-slip against dip-slip kinematics along the faults. The change from the ST1 to ST2 stress regimes reflects the significant clockwise rotation in the palaeo-Pacific plate subduction direction and defines the switching time at c. 119 Ma as precisely obtained by the lamprophyre dating.
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
References
- 5
- Cited by


