1. Introduction
Inbreeding is defined as the identity-by-descent (IBD) probability at any given autosomal locus and results from the mating of related individuals (Wright, Reference Wright1922; Malécot, Reference Malécot1948). The effects of inbreeding on traits of interest have been associated with substantial changes in phenotypic expectation and genetic variability (Falconer & Mackay, Reference Falconer and Mackay1996; Pannell, Reference Pannell2008). More specifically, Mendelian sampling variance decreases with inbreeding, and reductions in fitness would therefore be expected due to the higher phenotypic expression of deleterious recessive genes (Falconer & Mackay, Reference Falconer and Mackay1996). In domestic species, this fitness impairment has been revealed for multiple traits of interest, including birth weight (Norberg & Sørensen, Reference Norberg and Sørensen2007), growth (Pariacote et al., Reference Pariacote, Van Vleck and MacNeil1998; Fernández et al., Reference Fernández, Rodrigáñez, Toro, Rodríguez and Silió2002), litter size (Farkas et al., Reference Farkas, Curik, Csató, Csörnyei, Baumung and Nagy2007; Norberg & Sørensen, Reference Norberg and Sørensen2007), milk production (Miglior et al., Reference Miglior, Burnside and Kennedy1995; Mc Parland et al., Reference Mc Parland, Kearney, Rath and Berry2007) and longevity (Sewalem et al., Reference Sewalem, Kistemaker, Miglior and Van Doormaal2006).
Some researchers have proposed an alternative way to account for inbreeding depression by modelling founder-specific partial inbreeding coefficients instead of analysing the overall inbreeding of each individual (Rodrigáñez et al., Reference Rodrigáñez, Toro, Rodriguez and Silió1998; Gulisija et al., Reference Gulisija, Gianola, Weigel and Toro2006). This approach allows substantial heterogeneity of inbreeding depression effects in inbred descendants. This founder-related heterogeneity revealed a wide range of neutral and negative (and even positive) effects on litter size in swine (Rodrigáñez et al., Reference Rodrigáñez, Toro, Rodriguez and Silió1998), milk yield in dairy cattle (Gulisija et al., Reference Gulisija, Gianola, Weigel and Toro2006) and birth weight in meat-type sheep (Casellas et al., Reference Casellas, Piedrafita, Caja and Varona2009). Nevertheless, this research was focused on a few well-characterized founders with a large number of inbred descendants, with estimates being circumscribed to a relatively unrepresentative scenario that does not allow accurate extrapolations to entire populations.
Among the substantial profit of founder-specific inbreeding depression (FSID) estimates, inferences based on their expected distribution provide a more robust analysis and allow direct characterization of the inbreeding depression pattern and its biological relevance to the analysed population. Moreover, modelling FSID under the assumption of a given parametric distribution would increase model robustness and permit unbiased estimates even for founders with few data (Robinson, Reference Robinson1991). Note that this phenomenon cannot be easily modelled given the skew pattern of FSID (Rodrigáñez et al., Reference Rodrigáñez, Toro, Rodriguez and Silió1998; Gulisija et al., Reference Gulisija, Gianola, Weigel and Toro2006; Casellas et al., Reference Casellas, Piedrafita, Caja and Varona2009), where a standard symmetrical-Gaussian prior could originate abnormal model fits. Recent developments focused on the implementation of skew distributions in biological data analysis (Zhang et al., Reference Zhang, Montooth, Wells, Clark and Zhang2005; Varona et al., Reference Varona, Mekkawy, Gianola and Blasco2006, Reference Varona, Ibáñez-Escriche, Quintanilla, Noguera and Casellas2008) have opened a very appealing way to model asymmetry within the context of mixed models. More specifically, the skew patterns implemented by Sahu et al. (Reference Sahu, Dey and Branco2003) in the Gaussian distribution, allow left- or right-tail overexpressions with the only inclusion of just one additional parameter.
Sow longevity is a trait of major relevance for the swine industry (Serenius & Stalder, Reference Serenius and Stalder2004; Serenius et al., Reference Serenius, Stalder, Baas, Mabry, Goodwin, Johnson, Robinson, Tokach and Miller2006; Tarrés et al., Reference Tarrés, Bidanel, Hofer and Ducrocq2006), with relevant implications on both economic and welfare grounds. Although most of the genetic and environmental sources of variation in this trait have been extensively analysed in recent years, the effect of inbreeding on sow longevity remains unknown. Inbreeding depression has previously been related to longevity traits in dairy cattle (Sewalem et al., Reference Sewalem, Kistemaker, Miglior and Van Doormaal2006), deer (Sternicki et al., Reference Sternicki, Szablewski and Szwaczkowski2003), beetles (Fox et al., Reference Fox, Scheibly, Wallin, Hitchcock, Stillwell and Smith2006) and Drosophila (Vermeulen & Bijlsma, Reference Vermeulen and Bijlsma2004; Swindell & Bouzat, Reference Swindell and Bouzat2006), among others, but we lack available results for swine. Moreover, the effect of FSID on the longevity of domestic species has never been evaluated. The recent implementation of change-point baselines in survival analysis (Tarrés et al., Reference Tarrés, Casellas and Piedrafita2005, Reference Tarrés, Bidanel, Hofer and Ducrocq2006) and the inclusion of the change points as unknown parameters in the model (Casellas, Reference Casellas2007) allow a direct and straightforward characterization of the aging process of the analysed population within a parametric framework. Indeed, this approach reduced model parameterization when compared with semi-parametric methodologies (Cox, Reference Cox1972) and provides a vast increase in terms of model flexibility to address longevity data. In the present study, we assumed the methodology developed by Casellas (Reference Casellas2007) given its reasonable flexibility to fit longevity data as well as the integrated estimation of the change points. Although previous analyses with the Casellas (Reference Casellas2007) model were focused on systematic and additive genetic effects, this hierarchical approach can be easily expanded to account for additional sources of variation such as inbreeding-related effects governed by a set of different prior distributions.
Within this context, the aim of the present study was to analyse sow longevity and the impact of the effect of FSID on a Landrace population, with special emphasis on the characterization of the distribution pattern of FSID and its implications for sow longevity and breeding programmes.
2. Materials and methods
(i) Sow longevity data source
Longevity data for 4226 hyperprolific Landrace sows (mean±S.D., 13·3±7·2 piglets per litter) were recorded between 1988 and 2006 at a breeding farm (COPAGA S.C.C.L., Solsona, Spain). These sows were kept in standard farm facilities under standard management conditions, and all relevant reproductive and productive data were appropriately recorded (including date of mating, parturition and weaning, total number of piglets born, numbers of live and still births and weaned piglets, among others). Sow longevity was measured as the time interval (in days) between the first mating and culling or death (complete records), whereas records for sows that were still alive at the end of the data collection period were considered censored (Cox, Reference Cox1972). Except for the first few years when voluntary culling was minimized to increase population size (Table 1), the culling criteria remained the same throughout the period of data collection. As expected, average longevity was abnormally high for first cohorts of sows because old sows were retained in order to increase the population size (1604 days for sows firstly mated between years 1988 and 1990), whereas in subsequent years this average quickly decreased to reach average longevities ranging between 438 days (1995) and 691 days (1998). This heterogeneity falls within the range of previous studies in sows (Brandt et al., Reference Brandt, von Brevern and Glodek1999; Yazdi et al., Reference Yazdi, Rydhmer, Ringmar-Cedererg, Lundeheim and Johansson2000; Tarrés et al., Reference Tarrés, Bidanel, Hofer and Ducrocq2006). Sows were mainly culled when either (i) their biological status did not allow any additional reproductive cycles (i.e. insufficient body condition, illness, severe deficiencies in leg or teat condition) or (ii) their reproductive performance was unsatisfactory (i.e. sows that failed to become pregnant after successive inseminations, that produced small litters or that performed poorly at weaning). Indeed, this population has undergone a selection experiment for prolificacy (Noguera et al., Reference Noguera, Varona, Babot and Estany2002a, Reference Noguera, Varona, Babot and Estanyb) between 1993 and 1998 across three successive generations, although culling criteria did not change during this period. Nevertheless, the genetic trend obtained for the number of piglets born alive (≈0·5 piglets per litter) could have modulated the effect of the number of weaned piglets included in our analysis (see below). The overall survival probability for this Landrace population was characterized by the non-parametric Kaplan–Meier method (Kaplan & Meier, Reference Kaplan and Meier1958).
Table 1. Number of longevity records (n), percentage of censoring, and average longevity (±S.E.) according to years of first mating
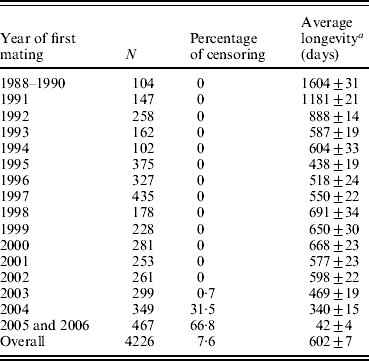
a Censored records were not considered.
Full pedigree included 6355 individuals with 458 boars and 5897 sows, 1082 of which were considered founders without known ancestors (177 boars and 905 sows). This population was founded from the acquisition of sows and boars from two different origins plus an additional incorporation of foreign individuals during the mid-1990s. After founder generation, pedigree data were accurately registered and parents are known for all boars and sows born in this population. Only 346 boars had progeny with registered longevity, with an average of 12·1±16·0 daughters per boar (mean±S.D.). This value ranged from 1 to 166 daughters per boar. Although mating between close relatives was avoided whenever possible, inbreeding occurred in successive generations. Moreover, separate breeding lines were generated (see Noguera et al., Reference Noguera, Varona, Babot and Estany2002b) and partially fused at the end of the selection experiment for hyperprolific sows. This population had overlapped generations, pedigree extending over 9–14 generations for gilts born in 2006. Table 1 shows the number of records and average longevity according to the year of first mating and also the percentage of censored data.
(ii) Inbreeding and partial inbreeding coefficients
Following Wright (Reference Wright1922) and Malécot (Reference Malécot1948), the inbreeding coefficient for the ith non-founder individual (F i) can be defined as the IBD probability at any given neutral locus, and is easily calculated as half the relationship coefficient between i's parents. Although F i has been widely used in the animal breeding literature, it does not provide detailed information about the contribution of each founder to the IBD probability. If founder-specific inbreeding coefficients are considered, F i can be partitioned as 
, where F ij is the IBD probability due to the jth founder on the ith individual and f is the number of founders contributing to i (Lacy et al., Reference Lacy, Alaks and Walsh1996; Rodrigáñez et al., Reference Rodrigáñez, Toro, Rodriguez and Silió1998). These F ij can be easily calculated following Gulisija et al. (Reference Gulisija, Gianola, Weigel and Toro2006) via partial coancestry matrices.
In our data set, 35 founders contributed inbred descendants although only 22 of them contributed more than 150 inbred sows with longevity data. These 22 founders were distributed among the three origins of foreign individuals and all of them had first-generation descendants with longevity data. Of these 22 founders, four couples of founders were fused into 4 virtual founders because each couple only contributed one offspring to the pedigree. FSID was evaluated on 14 founders and 4 virtual founders in order to assess the effects of FSID on sow longevity, with an extra level grouping the remaining 13 less-represented founders that contributed inbred descendants. Note that these 13 underrepresented founders originated inbreeding at a very low level and they were grouped to avoid model instability, mainly when a vague flat prior was assumed for inbreeding-related effects. To evaluate potential colinearity between F ij, pairwise correlation coefficients between F ij coefficients were estimated using the SAS Correlation procedure (v.9.1; Statistical Analysis Systems (SAS) Institute, Cary, NC, USA).
The analysed Landrace herd showed an average inbreeding percentage of 0·52±0·01%, although only 1198 of the sows with phenotypic data (28·4%) were inbred (F i>0; inbreeding coefficients ranged between 0·09 and 25%). Figures 1 a and 1 b show the average and maximum levels of inbreeding for Landrace sows per year at first mating. It can be observed that inbreeding appeared early in this population (sows born in 1991 or at the end of 1990) and showed an irregular increase from 1994 onwards. Within-year average inbreeding was less than 1%, with the exception of the sows firstly mated in 2004 for which the average value was 1·37% (Fig. 1 a). Maximum inbreeding fluctuated between 2·86 and 12·33% during the period 1994–2005, although the highest value (25%) was reached in 1991 (Fig. 1 b). These values agreed with those reported by Rathje (Reference Rathje2000) for other commercial and selected pig populations. Note that these irregular patterns could be due to the selection experiment carried out during the 1990s with two separate breeding lines fused in the year 1998, at the end of the experimental selection procedure (Noguera et al., Reference Noguera, Varona, Babot and Estany2002b).
Fig. 1. Average (a) and maximum (b) inbreeding of Landrace sows by years of first mating.
(iii) Statistical analyses
(a) Proportional hazards model
Within the context of the change point models introduced by Nguyen et al. (Reference Nguyen, Rogers and Walker1984) and Noura & Read (Reference Noura and Read1990) for survival analysis, sow longevity data were analysed under a change-point Weibull proportional hazards model with unknown change points (Casellas, Reference Casellas2007). The applied methodology was a Bayesian implementation of the change-point models adopted by Tarrés et al. (Reference Tarrés, Casellas and Piedrafita2005) and previously suggested by Yazdi et al. (Reference Yazdi, Visscher, Ducrocq and Thompson2002), assuming a common shape parameter throughout the parametric space, whereas the scale parameter could change at each predefined time-dependent period. This change-point characterization must be viewed as a simplified version of the Tarrés et al. (Reference Tarrés, Bidanel, Hofer and Ducrocq2006) model where all the parameters of the Weibull baseline change at a given change point. Moreover, omitting the different treatment of the change points in the models described by Tarrés et al. (Reference Tarrés, Bidanel, Hofer and Ducrocq2006) and Casellas (Reference Casellas2007), Tarrés et al. (Reference Tarrés, Bidanel, Hofer and Ducrocq2006) is more parameterized and thus advantages in model flexibility would be lost due to a greater penalization for overparameterization. Casellas (Reference Casellas2007) methodology was preferred given that it is based on a well known and long used extension of a regular Weibull model where an extra time-dependent effect is included to increase flexibility (Ducrocq et al., Reference Ducrocq, Quaasm, Pollak and Casella1988; Yazdi et al., Reference Yazdi, Visscher, Ducrocq and Thompson2002; Tarrés et al., Reference Tarrés, Casellas and Piedrafita2005; Casellas et al., Reference Casellas, Tarrés, Piedrafita and Varona2006). Following the standard survival model described by Cox (Reference Cox1972), the hazard (h i(t; xi, zi)) function at time t for a given sow i influenced by a set of systematic (b1 and b2), permanent environmental (p), inbreeding depression (d) and additive genetic (a) effects can be written as:
where x1i, z2i and z3i (x2i(t) and z1i(t)) are appropriate column vectors of incidences linking b1, d and a time-independent effects (b2 and p time-dependent effects), respectively. Following Casellas (Reference Casellas2007), h 0(t) is the baseline hazard function with the form h 0(t)=λρ(λt)ρ−1ξk for τk<t⩽τk+1 and k∊1, …, m. Note that y i is the longevity record of sow i, λ and ρ are the parameters of a Weibull distribution, ξk is the time-dependent effect between change points τk and τk+1, m is the number of change points, and τm+1 is the longest observed lifetime in the data set.
More specifically, b1 accounted for the time-independent effect of year at first mating with 16 levels (the years 1988–1990 and 2005–2006 were grouped; see Table 1) and b2 accounted for the time-dependent effect of the number of weaned piglets with 8 levels (gilts, 1–6 piglets, 7 piglets, 8 piglets, 9 piglets, 10 piglets, 11 piglets and more than 11 piglets) following Tarrés et al. (Reference Tarrés, Bidanel, Hofer and Ducrocq2006). Note that b2 was a time-dependent effect that was changed (if required) at each weaning date. In addition, p was a random time-dependent year–season effect with 71 levels. Year at first mating and year–season effects were required to account for involuntary heterogeneity in culling decisions during the analysed period, as well as for the voluntarily relaxed culling criteria during the first few years (Table 1).
(b) Likelihood and prior specifications
Five different models were analysed depending on the structure of vector d and its prior distribution. The most standard approach assumed d as a scalar element (improper uniform prior) accounting for the overall effect of inbreeding depression on sow longevity (model U1). Alternatively, d was a 19×1 column vector containing the founder-specific (14 founders, 4 virtual founders and 1 extra category for the less-contributing founders) estimates of inbreeding depression under five different a priori distributions: improper uniform distribution (model U19), symmetric normal distribution with mean fixed at zero (model SN019), symmetric normal distribution with mean μ (SNμ19), asymmetric normal distribution with mean fixed at 0 (model AN019) and asymmetric normal distribution with mean μ as an additional unknown in the model (model ANμ19).
Taking model ANμ19 as a starting point, the joint posterior distribution of all the parameters conditional to the data was proportional to the likelihood multiplied by the prior distribution of the parameters,
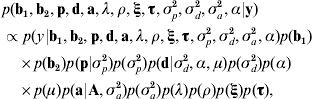
where ξ and τ are the column vectors of baseline-related time-dependent effects and change points, respectively; σp2, σd2 and σa2 are the permanent environmental, inbreeding depression and additive genetic variance components, respectively; A is the numerator relationship matrix, and α is the asymmetry parameter related to d (see below). Under the assumption that censoring was independent and non-informative, the likelihood was stated as described by Allison (Reference Allison1995) and Casellas (Reference Casellas2007).
The recent development of skew-elliptical distributions (Sahu et al., Reference Sahu, Dey and Branco2003; Sahu & Chai, Reference Sahu and Chai2005) has allowed the implementation of a skew-Gaussian prior distribution for d,
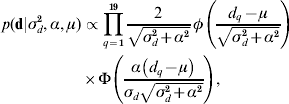
where d q is the qth element in d, α is the degree of asymmetry defined in real space, and φ( ) and Φ( ), respectively, denote the density function and cumulative density function of a standard normal distribution with arguments as defined in parentheses. This assumption is of special relevance to this particular research because it allows a straightforward characterization of the posterior distribution of d in terms of symmetric (α=0) patterns, or right-tail (left-tail) overexpressions when α>0 (α<0). Note that the first and second moments of the posterior distribution of d can be directly calculated from 
and Var(d)=σd2+α2[1−(2/π)], respectively (Sahu et al., Reference Sahu, Dey and Branco2003). A priori distributions for p and a vectors were stated as p(p|σp2)∝N(0, Ipσp2) and p(a|A,σa2)∝N(0, Aσa2), where Ip is an identity matrix with dimensions equal to the number of elements in p. Note that relationship matrix A was constructed following Westell et al. (Reference Westell, Quaas and Van Vleck1988) to account for the different origins of the founder individuals. As previously reported by Damgaard & Korsgaard (Reference Damgaard and Korsgaard2006), Casellas (Reference Casellas2007) and Varona et al. (Reference Varona, Ibáñez-Escriche, Quintanilla, Noguera and Casellas2008), a priori model parameters ρ, λ, ξ, σp2, σd2, σa2, α and the elements of b1 and b2 were assumed to be mutually independent with improper flat priors. The prior distribution for τ assumed that change points were distributed as order statistics from a uniform distribution on the interval [0, τm+1], where τ1=0<τ2< … <τm<τm+1 (Casellas, Reference Casellas2007). The prior distribution of μ was assumed to be improper flat. This model was reduced to AN019 by fitting μ=0. In this case, the a priori probability of d was conditioned to σd2 and α. All the remaining a priori distributions were stated as for model ANμ19 (see above for a detailed description of these priors).
For model SN019, the posterior distribution was identical to the posterior distribution of model AN019 after the arbitrarily fit α=0. In a similar way, the posterior distribution for model SNμ19 fitted α=0 and assumed p(d|σd2, μ)∝N(μ, Idσd2), where Id is a 19×19 identity matrix, and an improper flat prior for p(μ). The posterior distribution for models U1 and U19 were assumed as in the previous model, with the exception of p(d), which had an improper flat distribution.
(c) Markov chain Monte Carlo sampling and model comparison
Preliminarily, each model (U1, U19, SN019, SNμ19, AN019 and ANμ19) was analysed six times, from no change points to 5 change points, and the appropriate number of change points was established by comparing model performance in terms of the deviance information criterion (DIC; Spiegelhalter et al., Reference Spiegelhalter, Best, Carlin and van der Linde2002). Models with smaller DIC were favoured as this indicates a better fit and lower degree of model complexity (Spiegelhalter et al., Reference Spiegelhalter, Best, Carlin and van der Linde2002). In general, differences larger than 3–5 DIC units are typically assumed as relevant (Spiegelhalter et al., Reference Spiegelhalter, Best, Carlin and van der Linde2002, Reference Spiegelhalter, Thomas, Best and Lunn2003). In all chases, DIC reached its smaller value for models with 3 change points, it being 4·1–7·4 DIC units smaller than the second best model (4 change points; results not shown). Within this context, further analyses were focused on the basis of models with 3 change points, and alternative prior specifications for d were compared with DIC.
Five independent chains of 1 000 000 rounds were launched for each model and the first 50 000 iterations were discarded as burn-in (Raftery & Lewis, Reference Raftery, Lewis, Bernardo, Berger, Dawid and Smith1992). Metropolis–Hastings sampling (Metropolis et al., Reference Metropolis, Rosenbluth, Rosenbluth, Teller and Teller1953; Hastings, Reference Hastings1970) and Gibbs sampling (Gelfand & Smith, Reference Gelfand and Smith1990) procedures were used to sample from the marginal posterior distribution of all the unknowns in the models. A uniform proposal distribution with mathematical expectation at the current value of each parameter was used for Metropolis–Hastings sampling. The range of the proposed distribution for each parameter was determined in a preliminary analysis, with an acceptance rate of greater than 20% for all parameters. Given the high autocorrelation between successive samples related to the Metropolis–Hastings method, a total of 19 000 samples of model parameters were saved from each chain with a lag interval of 50 iterations.
3. Results and discussion
(i) Partial inbreeding coefficients in the analysed Landrace population
As described above, partial inbreeding coefficients were estimated for 14 founders, 4 virtual founders (couples of founders considered together) and an extra level corresponding to the remaining 13 founders, which contributed a few inbred descendants. Each founder (or group of founders) contributed between 160 and 1162 inbred descendants with an average partial inbreeding coefficient of 0·003 and 0·11%, even though (within-founder) maximum values oscillated between 0·39 and 25% (results not shown in the tables). This variability indicated that the breeding strategies applied to this herd resulted in unequal contribution of founder genomes to overall inbreeding, as previously described in other species (Gulisija et al., Reference Gulisija, Gianola, Weigel and Toro2006; Casellas et al., Reference Casellas, Piedrafita, Caja and Varona2009). Correlations for partial inbreeding coefficients between pairs of founders ranged from −0·01 (P=0·672) to 0·25 (P=0·048), suggesting a small or null incidence of potential biases due to colinearity.
(ii) Empirical assessment of Landrace sow longevity
Figure 2 shows the empirical Kaplan–Meier (Kaplan & Meier, Reference Kaplan and Meier1958) survival function for the analysed Landrace population. The Kaplan–Meier survival function showed a pseudo-cyclic pattern with peaks each ~140 days during the first 500 days of productive life. These falls started at day 20 (3 weeks after the first mating), and could have been related to a substantial culling of gilts that failed to become pregnant during their first heats. After that, the observed reduction in the cycle every ~140 days may have matched the end of each reproductive cycle (gestation ~114 days; weaning period ~25 days), as previously reported by Serenius et al. (Reference Serenius, Stalder, Baas, Mabry, Goodwin, Johnson, Robinson, Tokach and Miller2006), Tarrés et al. (Reference Tarrés, Bidanel, Hofer and Ducrocq2006) and Fernández de Sevilla et al. (Reference Fernández de Sevilla, Fàbrega, Tibau and Casellas2008). After day 500, survival probability showed a smooth trend with a long tail extending for longevities of greater than 2000 days. The average length of the productive life of sows was then 524 days (1 year and 5 months) with an annual replacement rate of 69·7%. Note that this average longevity (replacement rate) was substantially shorter (greater) than those reported in other populations such as Landrace sows (Yazdi et al., Reference Yazdi, Rydhmer, Ringmar-Cedererg, Lundeheim and Johansson2000; 617 days), Large White×Landrace crossbred sows (Le Cozler et al., Reference Le Cozler, Dagorn, Lindberg, Aumaitre and Dourmand1998; ~1000 days), Large White sows (Tarrés et al., Reference Tarrés, Bidanel, Hofer and Ducrocq2006; 602 days) and crossbred sows (Brandt et al., Reference Brandt, von Brevern and Glodek1999; 880 days).
Fig. 2. The Kaplan–Meier (Kaplan & Meier, Reference Kaplan and Meier1958) survival function for the analysed Landrace population.
(iii) Model comparison, change-point baseline function and genetic background
The DIC statistic allowed straightforward comparison across models (Table 2). Model AN019 was preferred on account of its smaller DIC values, although differences with ANμ19 were small and almost negligible. Within this context, the small advantage showed by model AN019 in front of model ANμ19 was not conclusive, although the reduction in model parameterization proposes AN019 as a more parsimonious choice. This small difference in terms of model performance could be due to the small estimate obtained for μ under model ANμ19 (mode=0·003). DICs suggested that model AN019 achieved a better fit to sow longevity data when compared with models U1, U19, SN019 and SNμ19. The small empirical S.E. obtained for average DIC estimates (~1 DIC unit) corroborated the relevance of these differences, ranging between 3·7 DIC units (AN019 against SNμ19) and 16·0 DIC units (AN019 against U1). Note that these magnitudes fell within the range of statistically relevant differences suggested by Spiegelhalter et al. (Reference Spiegelhalter, Best, Carlin and van der Linde2002, Reference Spiegelhalter, Thomas, Best and Lunn2003). Within this context, using partial inbreeding coefficients seems the best way to model inbreeding depression in domestic species, as previously suggested by Casellas et al. (Reference Casellas, Piedrafita, Caja and Varona2009). Furthermore, DIC differences between models U19, SN019, SNμ19, AN019 and ANμ19 (Table 2) suggested that the restrictions imposed by the skew-normal prior on inbreeding depression effects were preferable to the symmetric pattern and were probably more robust than analysis with the improper flat prior. In a similar way, models SNμ19, AN019 and ANμ19 allowed for non-null centrality parameters for FSID effects, this increased flexibility being also preferred in terms of DIC (Table 2). In conclusion, model AN019 was preferred given that it was less parameterized than model ANμ19 and clearly reached a smaller DIC than the remaining models.
Table 2. Model comparison in terms of mean (empirical S.E.) of the DIC (Spiegelhalter et al., Reference Spiegelhalter, Best, Carlin and van der Linde2002). All models addressed three additional change points in the baseline function
Baseline parameters for model AN019 are shown in Table 3. The Weibull pattern showed a ρ value of 0·93, close to an exponential form, whereas λ was small (8×10−5; models U1, U19, SN019, SNμ19 and ANμ19 converged at approximately the same values). Modal estimates (and the highest posterior density region at 95% (HPD95)) for change points in the model AN019 were located at 296 days (289–300 days), 492 days (477–499 days) and 1012 days (1088–1017 days), and the hazard ratio significantly increased with the age of the sow (Table 3). More interestingly, the additive genetic variance for sow longevity was close to 0·31, suggesting a moderate to low genetic background for this trait (h 2=0·16). Our heritability estimate agreed with those cited by López-Serrano et al. (Reference López-Serrano, Reinsch, Looft and Kalm2000) and Yazdi et al. (Reference Yazdi, Rydhmer, Ringmar-Cedererg, Lundeheim and Johansson2000) and suggested that sow longevity could be effectively improved in this population through genetic selection.
Table 3. Baseline parameter estimates for each analysis of model AN019 (0–5 change points in the model): mode (HPD95) of the posterior distribution
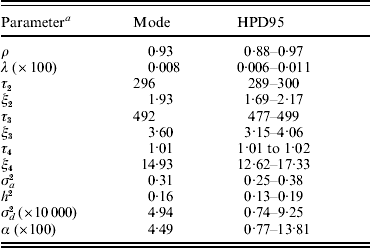
a The variables ρ and λ are the parameters of the Weibull distribution; ξk is the time-dependent effect between change points τk and τk+1; σa2 and σd2 are the additive genetic and inbreeding depression variance components, respectively; heritability (h 2) was calculated as h 2=σa2/[σa2+(π2/6)]; α is the asymmetry parameter for inbreeding depression effects.
(iv) Inbreeding depression effects and distribution pattern
Assuming partial inbreeding coefficients in terms of percentage, model AN019 suggested substantial heterogeneity for d effects (Fig. 3). The 19 founder elements contributing to inbreed descendants showed positive modal estimates for the posterior distribution of the regression coefficients in vector d, except for two elements that showed negative modes (Fig. 3). Given the form of eqns (1) and (2), positive estimates reduced sow longevity, whereas negative estimates implied an increase in the length of productive life (Allison, Reference Allison1995). More specifically, the greatest effect in d reached a mode of 0·076 for each 1% increase in inbreeding, which suggested that the hazard probabilities were respectively 1·08 and 2·14 times greater for 1% and 10% inbred individuals (founder-specific partial inbreeding coefficient) in comparison with outbred sows. In our case, these increases in hazard probabilities are equal to a reduction in sow longevity of 32 and 167 days, respectively. The majority of modal values for d elements were grouped around 0·03, the same value as that obtained by the U1 model for the modal estimate of overall inbreeding depression on sow longevity (0·032; HPD95 ranged between −0·002 and 0·065) and close to the modal estimate obtained for μ in model SNμ19 (0·027; HPD95 ranged between −0·011 and 0·053). As expected, estimates of d suffered from low precision and provided wide HPD95 due to the limited amount of available information with which to estimate each parameter. Given the selection experiment on sow prolificacy carried out in this population during three generations, an uncontrolled contribution of the selection scheme on d estimates cannot be completely discarded. Note that sow prolificacy may also be influenced by inbreeding and, consequently, longevity of inbred animals may have been genetically modified by involuntary selection and not only by loss of fitness. This uncontrolled contribution must be ruled by a substantial genetic correlation between sow longevity and prolificacy traits (Tholen et al., Reference Tholen, Bunter, Hermesch and Graser1996; Serenius & Stalder, Reference Serenius and Stalder2004).
Fig. 3. FSID effects on sow longevity obtained through model AN019 (the point represents the modal estimate; the whiskers show the range of the HPD95).
The most relevant result from this research was the general pattern described by the joint posterior distribution of elements in d under model AN019 with 3 change points. This posterior distribution was straightforwardly characterized by σd2 and α parameters, with both being positive and significantly different from zero (Table 3). Considering modal estimates, the joint posterior distribution of d describes a right-sided overexpressed distribution with its mode located at 0·034 (Fig. 4), agreeing with the dispersion of the d elements that is roughly shown in Fig. 3, as well as with the modal estimate obtained under model U1. This distribution (model AN019) had a mean of 0·036, an S.D. of 0·032 (see equations in section 2) and an asymmetry parameter of 0·045, and reported 85·2% of positive estimates (with a negative effect on sow longevity) for the elements in d. Posterior asymmetry under model AN019 is clearly characterized in Fig. 4, with 59·3% of probability placed on the right-hand side of the modal estimate. Note that Sahu's approach (Sahu et al., Reference Sahu, Dey and Branco2003), which is shown in eqn (3), substantially increased the flexibility of the standard-Gaussian prior typically assumed for random effects in mixed models, allowing for asymmetry and also for non-zero modal estimates, as previously reported by Varona et al. (Reference Varona, Ibáñez-Escriche, Quintanilla, Noguera and Casellas2008).
Fig. 4. Predicted distribution of the FSID effects under model AN019.
The results obtained in this study also highlight that heterogeneity in inbreeding depression effects is an important phenomenon with a relevant impact on sow longevity, and therefore also on the economics of the swine industry. Heterogeneity in inbreeding depression effects has previously been reported in the productive and reproductive traits of sows (Rodrigáñez et al., Reference Rodrigáñez, Toro, Rodriguez and Silió1998), dairy cows (Gulisija et al., Reference Gulisija, Gianola, Weigel and Toro2006) and ewes (Casellas et al., Reference Casellas, Piedrafita, Caja and Varona2009), although their impact and expected distribution pattern had never been studied in relation to the longevity of domestic breeds. The overall effect of inbreeding depression on animal life span has been typically reported as negative in experimental species (Vermeulen & Bijlsma, Reference Vermeulen and Bijlsma2004; Fox et al., Reference Fox, Scheibly, Wallin, Hitchcock, Stillwell and Smith2006; Swindell & Bouzat, Reference Swindell and Bouzat2006), wild species (Sternicki et al., Reference Sternicki, Szablewski and Szwaczkowski2003) and domestic species (Sewalem et al., Reference Sewalem, Kistemaker, Miglior and Van Doormaal2006), and this trend was confirmed in the present paper. Beyond this overall trend, this research has also shown a wide range of negative, neutral and even positive effects of inbreeding on sow longevity. These must be more carefully considered in further analyses and genetic evaluations in order to eliminate bias from mixed model solutions (Gulisija et al., Reference Gulisija, Gianola, Weigel and Toro2006). Negative and neutral effects can be easily related to the unevenly distribution of the deleterious recessive genetic load among the founder genomes or to the differential selection intensity applied to the different founder lines (Gulisija et al., Reference Gulisija, Gianola, Weigel and Toro2006), which partially supports the traditional assumption that inbreeding must be avoided in domestic livestock. Indeed, the founders acquired at different years could support the hypothesis of differential selection intensity applied to the different founder genomes. Within the context of dominance (recessive) effects, the positive effect may be associated with the fixation of favourable alleles and the purging of deleterious alleles from previous generations (MacKinnon, Reference MacKinnon2003), although this hypothesis needs to be confirmed by further studies. Indeed, positive effects of inbreeding have been previously reported in Drosophila melanogaster (Sánchez et al., Reference Sánchez, Toro and García1999; pupa size). Similarly, Weiner et al. (Reference Weiner, Lee and Woolliams1992) reported an increase in lamb birth weight, and Galal et al. (Reference Galal, Afifi, El-Kimary, Ahmad and Shawar1981) observed an increase in lamb survival, although both results were obtained under high values of inbreeding.
As a whole, our results allow a more accurate description of the effects of inbreeding depression phenomena and the expected distribution within a founder-specific framework. Beyond the particular estimation of inbreeding depression effects related to each founder, the assumption of an a priori skew-normal distribution for d allows a detailed characterization of the expected dispersion pattern of FSID effects, and also of their biological relevance for sow longevity.
The research contract of J. Casellas was partially financed by the Spanish Ministry of Education and Science (the Juan de la Cierva programme) within the framework of the project AGL2004-08368-CO3. Financial support was provided by the IRTA (grant number IRTA21022). We are indebted to the staff of Nova Genètica and COPAGA SCCL and, in particular, to E. Ramells, F. Marquez, R. Malé and F. Rovira, for their technical support. We are also indebted to two anonymous referees for their helpful comments on the manuscript.
