Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-04T21:34:00.449Z Has data issue: false hasContentIssue false
  • English
  • Français

Prediction of rates of inbreeding in selected populations

Published online by Cambridge University Press:  14 April 2009

Naomi R. Wray  and
Robin Thompson
Naomi R. Wray
Affiliation:
Institute of Animal Genetics, University of Edinburgh, West Mains Road, Edinburgh EH9 3JN
Robin Thompson
Affiliation:
AFRC Institute of Animal Physiology and Genetics Research, Edinburgh Research Station, Roslin, Midlothian, EH25 9PS

Summary

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A method is presented for the prediction of rate of inbreeding for populations with discrete generations. The matrix of Wright's numerator relationships is partitioned into ‘contribution’ matrices which describe the contribution of the Mendelian sampling of genes of ancestors in a given generation to the relationship between individuals in later generations. 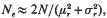These contributions stabilize with time and the value to which they stabilize is shown to be related to the asymptotic rate of inbreeding and therefore also the effective population size, where N is the number of individuals per generation and μr and 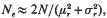are the mean and variance of long-term relationships or long-term contributions. These stabilized values are then predicted using a recursive equation via the concept of selective advantage for populations with hierarchical mating structures undergoing mass selection. Account is taken of the change in genetic parameters as a consequence of selection and also the increasing ‘competitiveness’ of contemporaries as selection proceeds. Examples are given and predicted rates of inbreeding are compared to those calculated in simulations. For populations of 20 males and 20, 40, 100 or 200 females the rate of inbreeding was found to increase by as much as 75% over the rate of inbreeding in an unselected population depending on mating ratio, selection intensity and heritability of the selected trait. The prediction presented here estimated the rate of inbreeding usually within 5% of that calculated from simulation.

Type
Research Article
Information
Genetics Research , Volume 55 , Issue 1 , February 1990 , pp. 41 - 54
Copyright
Copyright © Cambridge University Press 1990

References

Bulmer, M. G. (1971). The effect of selection on genetic variability. The American Naturalist. 105, 201–211.CrossRefGoogle Scholar
Bulmer, M. G. (1980). The Mathematical Theory of Quantitative Genetics. Clarendon Press, Oxford.Google Scholar
Burrows, P. M. (1984 a). Inbreeding under selection from unrelated families. Biometrics 40, 357–366.CrossRefGoogle Scholar
Burrows, P. M. (1984 b). Inbreeding under selection from related families. Biometrics 40, 895–906.CrossRefGoogle Scholar
Crow, J. F. & Denniston, C. (1988). Inbreeding and variance effective number. Evolution 42, 482–495.CrossRefGoogle Scholar
Crow, J. F. & Morton, N. E. (1955). The measurement of gene frequency in small populations. Evolution 9, 482–495.CrossRefGoogle Scholar
Dempster, E. R. & Lerner, I. M. (1950). Heritability of threshold characters. Genetics 35, 212–236.CrossRefGoogle ScholarPubMed
Hill, W. G. (1972). Effective size of populations with overlapping generations. Theoretical Population Biology 3, 278–289.CrossRefGoogle ScholarPubMed
Hill, W. G. (1979). A note on effective population size with overlapping generations. Genetics 92, 317–322.CrossRefGoogle ScholarPubMed
Hill, W. G. (1985). Fixation probabilities of mutant genes with artificial selection. Génétiques Selection et Evolution 17, 351–358.Google Scholar
James, J. W. & McBride, G. (1958). The spread of genes by natural and artificial selection in a closed poultry flock. Journal of Genetics 56, 55–62.CrossRefGoogle Scholar
Jones, L. P. (1969). Effects of artificial selection on rates of inbreeding in populations of Drosophila Melanogaster. I. Effect in early generations. Australian Journal of Biological Science 22, 143–155.CrossRefGoogle Scholar
Mendell, N. C. & Elston, R. C. (1974). Multifactorial traits: Genetic analysis and prediction of recurrence risks. Biometrics 30, 41–57.CrossRefGoogle ScholarPubMed
Nei, M. & Murata, M. (1966). Effective population size when fertility is inherited. Genetical Research 8, 257–260.CrossRefGoogle ScholarPubMed
Robertson, A. (1961). Inbreeding in artificial selection programmes. Genetical Research 2, 189–194.CrossRefGoogle Scholar
Thompson, R. (1977). The estimation of heritability with unbalanced data. II. Data available on more than two generations. Biometrics 33, 497–504.CrossRefGoogle Scholar
Tallis, G. M. (1987). Ancestral covariance and the Bulmer effect. Theoretical and Applied Genetics 73, 815–820.CrossRefGoogle ScholarPubMed
Woolliams, J. A. (1989). Modifications to MOET nucleus breeding schemes to improve rates of genetic progress and decrease rates of inbreeding in dairy cattle. Animal Production 49, 1–14.Google Scholar
Wray, N. R. (1989). Consequences of selection in closed populations with particular reference to closed nucleus herds of pigs. PhD thesis. University of Edinburgh.Google Scholar
Wright, S. (1922). Coefficients of inbreeding and relationship. American Naturalist 56, 330–338.CrossRefGoogle Scholar
Wright, S. (1931). Evolution in Mendelian populations. Genetics 16, 97–159.CrossRefGoogle ScholarPubMed
Yoo, B. H. (1980). Long-term selection for a quantitative character in large replicate populations of Drosophila melanogaster. V. The inbreeding effect of selection. Australian Journal of Biological Science 33, 713–723.Google Scholar