Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-23T10:34:17.375Z Has data issue: false hasContentIssue false
  • English
  • Français

Models of long-term artificial selection in finite population with recurrent mutation

Published online by Cambridge University Press:  14 April 2009

William G. Hill  and
Jonathan Rasbash
William G. Hill
Affiliation:
Institute of Animal Genetics, University of Edinburgh, West Mains Road, Edinburgh EH9 3JN
Jonathan Rasbash
Affiliation:
Institute of Animal Genetics, University of Edinburgh, West Mains Road, Edinburgh EH9 3JN
Rights & Permissions [Opens in a new window]

Summary

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

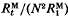The effects of mutation on mean and variance of response to selection for quantitative traits are investigated. The mutants are assumed to be unlinked, to be additive, and to have their effects symmetrically distributed about zero, with absolute values of effects having a gamma distribution. It is shown that the ratio of expected cumulative response to generation t from mutants, 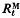, and expected response over one generation from one generation of mutants, , is a function of t/N, where t is generations and N is effective population size. Similarly, 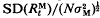, is a function of t/N, where 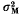is the increment in genetic variance from one generation of mutants. The mean and standard deviation of response from mutations relative to that from initial variation in the population, 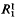in the first generation, are functions of . Evaluation of these formulae for a range of parameters quantifies the important role that population size can play in response to long-term selection.

Type
Research Article
Information
Genetics Research , Volume 48 , Issue 2 , October 1986 , pp. 125 - 131
Copyright
Copyright © Cambridge University Press 1986

References

Clayton, G. A. & Robertson, A. (1955). Mutation and quantitative genetic variation. American Naturalist 89, 151–158.CrossRefGoogle Scholar
Clayton, G. A. & Robertson, A. (1957). An experimental check on quantitative genetic theory. II. The long term effects of selection. Journal of Genetics 55, 152–170.CrossRefGoogle Scholar
Dudley, J. W. (1977). 76 generations of selection for oil and protein percentage in maize. In Proceedings of the International Conference on Quantitative Genetics (ed. Pollak, E., Kempthorne, O. and Bailey, T. B. Jr.), pp. 459–473. Ames: Iowa State University Press.Google Scholar
Frankham, R. (1980). Origin of genetic variation in selection lines. In Selection Experiments in Laboratory and Domestic Animals (ed. Robertson, A.), pp. 56–68. Slough: Commonwealth Agricultural Bureaux.Google Scholar
Hill, W. G. (1982). Predictions of response to artificial selection from new mutations. Genetical Research 40, 255–278.CrossRefGoogle ScholarPubMed
Hill, W. G. & Rasbash, J. (1986). Models of long term artificial selection in finite population. Genetical Research 48, 41–50.CrossRefGoogle ScholarPubMed
James, J. W. (1962). Conflict between directional and centripetal selection. Heredity 17, 487–499.CrossRefGoogle ScholarPubMed
Keightley, P. D. & Hill, W. G. (1983). Effects of linkage on response to directional selection from new mutations. Genetical Research 42, 193–206.CrossRefGoogle ScholarPubMed
Latter, B. D. H. (1966). Selection for a threshold character in Drosophila. II. Homeostatic behaviour on relaxation of selection. Genetical Research 8, 205–218.CrossRefGoogle ScholarPubMed
Lynch, M. & Hill, W. G. (1986). Phenotypic evolution by neutral mutation. Evolution (in the Press).Google Scholar
Lynch, M. (1986). The rate of polygenic mutation. Genetical Research (submitted).Google Scholar
Robertson, A. (1960). A theory of limits in artificial selection. Proceedings of the Royal Society of London B 153, 234–249.Google Scholar
Robertson, F. W. (1955). Selection response and the properties of genetic variation. Cold Spring Harbor Symposium on Quantitative Biology 20, 197–211.CrossRefGoogle ScholarPubMed
Yoo, B. H. (1980 a). Long term selection for a quantitative character in large replicate populations of Drosophila melanogaster. I. Response to selection. Genetical Research 35, 1–17.CrossRefGoogle Scholar
Yoo, B. H. (1980 b). Long term selection for a quantitative character in large replicate populations of Drosophila melanogaster. II. Lethals and visible mutants with large effects. Genetical Research 35, 19–31.CrossRefGoogle Scholar
Zeng, Z.-B. & Hill, W. G. (1986). The selection limit due to the conflict between truncation and stabilizing selection with mutation. Genetics (in press).CrossRefGoogle Scholar